Archives
February 2024
Categories
All
|
Back to Blog
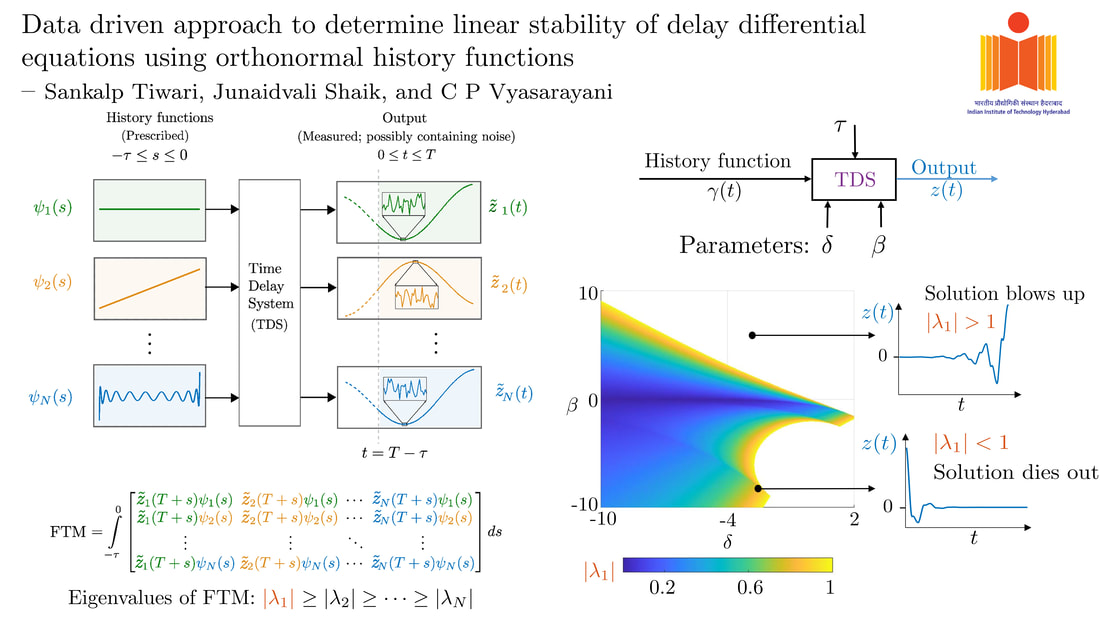
Sankalp Tiwari, Junaidvali Shaik, and C. P. Vyasarayani J. Comput. Nonlinear Dynam. Feb 2024, 19(2): 021002 https://doi.org/10.1115/1.4064251 Delayed systems are those in which the present dynamics is governed by what happened in the past. They are encountered in manufacturing, biology, population dynamics, control systems, etc. Determining stability of such systems is an important and difficult problem. In the existing works, stability is determined by assuming the governing differential equation. However, the equation may not be known or difficult to obtain. Unlike existing works, our method determines the linear stability of a delayed system using its response to a few known inputs. In particular, our method does not require or assume the differential equation governing that system. The only system information we use is its largest delay time, and the only assumption we make about the underlying equation is that its coefficients are either constant or time-periodic. Our approach involves giving the first few functions of an orthonormal polynomial basis as input and measuring/computing the corresponding responses to generate a state transition matrix, whose largest eigenvalue determines the stability. We demonstrate our method's correctness, efficacy, and convergence by studying four candidate DDEs with differing features. Importantly, we show that our approach is robust to noise in measurement, thereby establishing its suitability for practical applications.
0 Comments
Read More
Back to Blog
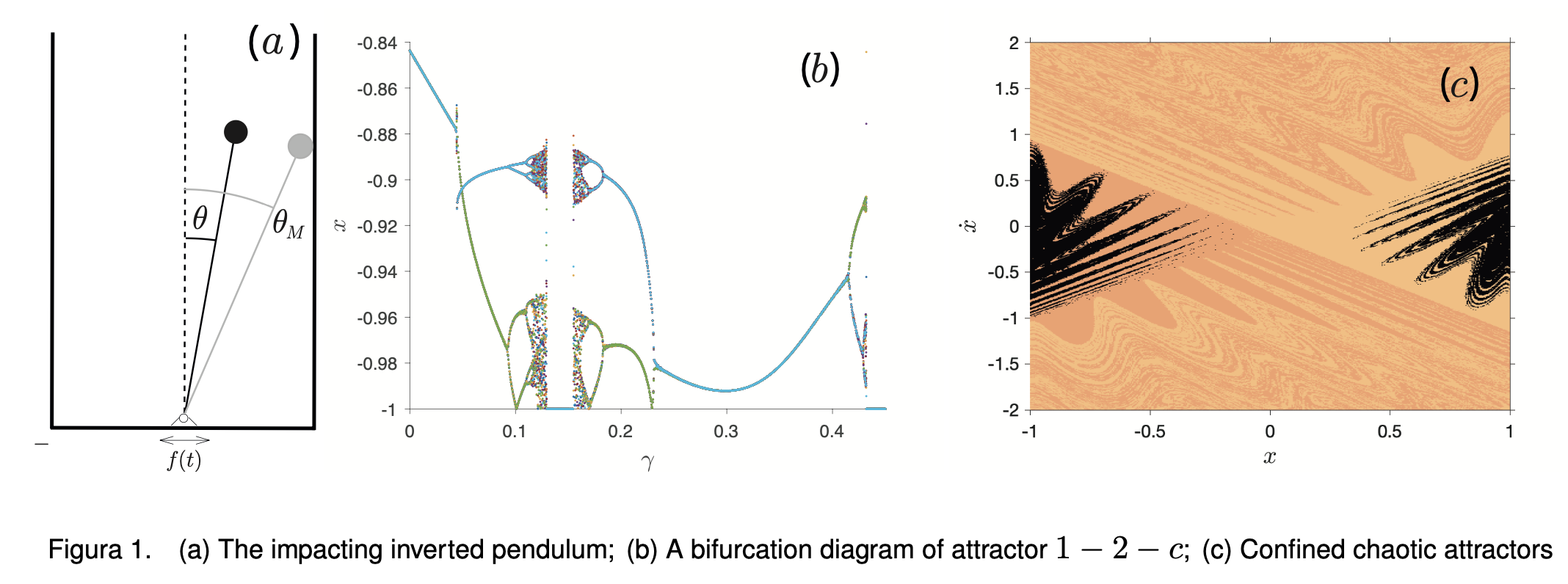
Milena Petrini, Lucio Demeio and Stefano Lenci ASME. J. Comput. Nonlinear Dyn. October 2023, 18(10): 101004 https://doi.org/10.1115/1.4063034 In this work we examine the nonlinear dynamics of an inverted pendulum between lateral rebounding barriers. We continue the numerical investigation started in (Demeio et al., 2006, “Response Scenario and Non-Smooth Features in the Nonlinear Dynamics of an Impacting Inverted Pendulum”, ASME J. Comput. Nonlin. Dyn., 1(1), pp. 56-64) by adding the contribution of the second harmonic in the external forcing term. We investigate the behavior of the periodic attractors by bifurcation diagrams with respect to each amplitude and by behavior charts of single attractors in the amplitude parameters plane for fixed frequency. We study the effects of the second harmonic term on the existence domain of each attractor, on local bifurcations and on the changes in the basins of attraction. The behavior of some robust chaotic attractor is also considered. In the evolution of the periodic attractors we have observed that the addition of the second harmonic generates a rich variety of behaviors, such as loss of stability and formation of isolas of periodic orbits. In the case of chaotic attractors, we have studied one attractor at high frequency, ω = 18, and one at low frequency, ω = 3. In the high frequency case we detect a transition from a scattered to a confined attractor, whereas at the lower frequency the chaotic attractor is present over a wide range of the second harmonic’s amplitude. Finally, we extend the investigation of the chaotic attractors by bifurcation diagrams with respect to the frequency.
Back to Blog
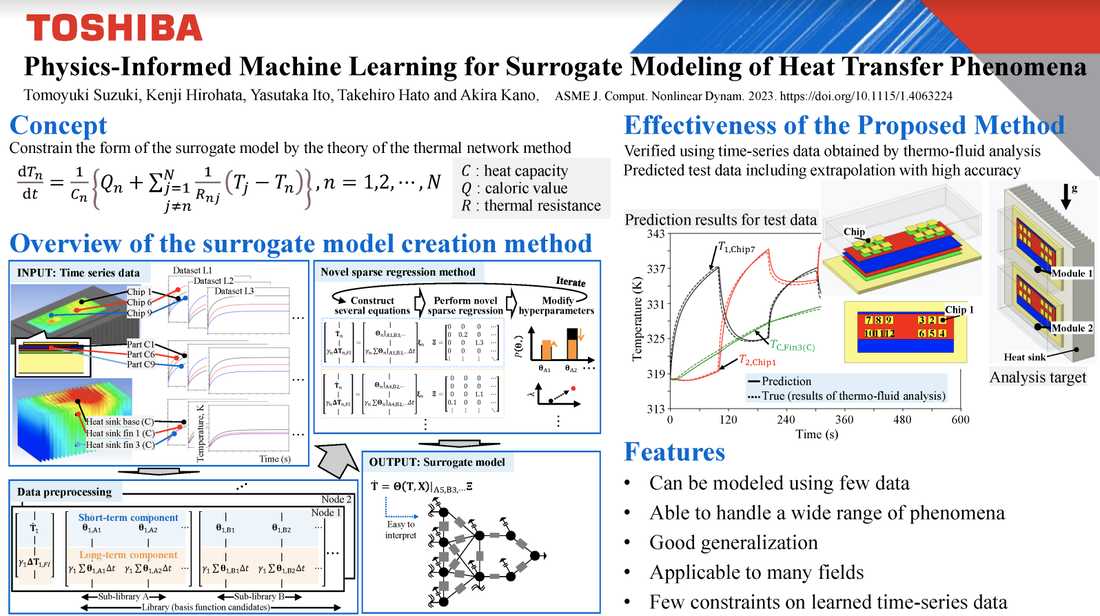
Tomoyuki Suzuki, Kenji Hirohata, Yasutaka Ito, Takehiro Hato, Akira Kano J. Comput. Nonlinear Dynam. November 2023, 18(11): 111001. https://doi.org/10.1115/1.4063224 This paper proposes a sparse modeling method for automatically creating a surrogate model for nonlinear time-variant systems from a small number of time-series data. The proposed method is an improvement over a method for sparse identification of nonlinear dynamical systems first proposed in 2016, for application to temperature prediction simulations. The form of the thermal model is constrained by the physical model, and we use three novel machine-learning methods to efficiently estimate the model parameters. We verify the proposed method’s effectiveness using time-series data obtained by thermo-fluid analysis of a power module mounted on a comb-shaped heat sink. The proposed method has potential applications in a wide range of fields where the concept of equivalent circuits is applicable. Because the proposed method requires few data, has high extrapolation accuracy, and is easily interpreted, we expect that design parameters can be fine-tuned and actual loads considered, and that condition-based maintenance can be realized through real-time simulations.
Back to Blog
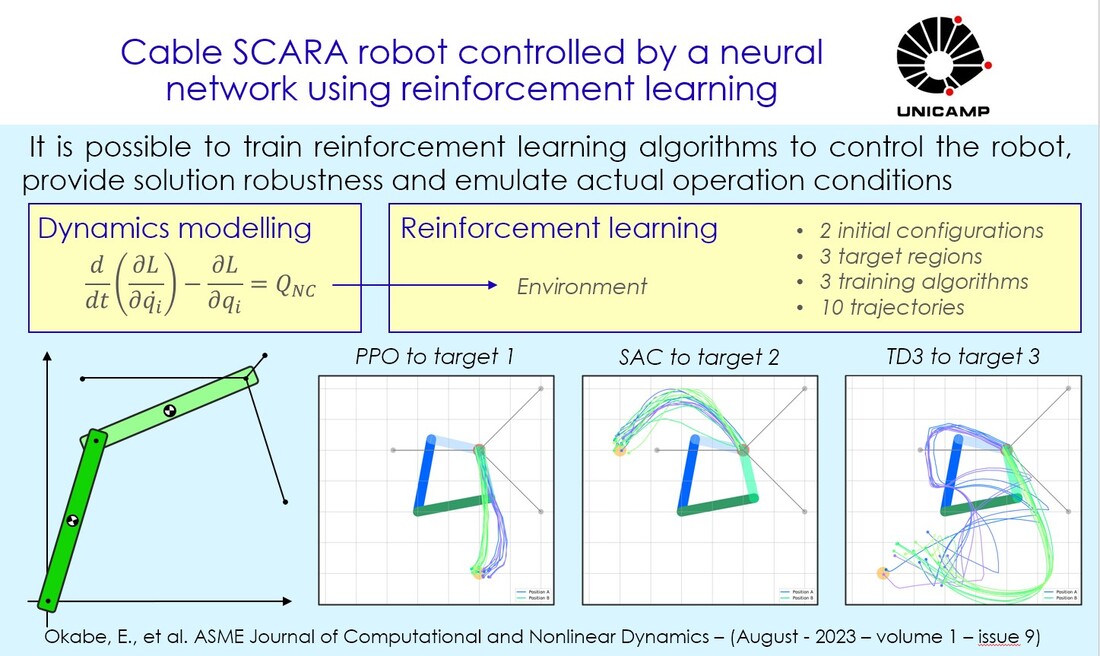
Eduardo Okabe, Victor Paiva, Luis Silva-Teixeira, Jaime Izuka J. Comput. Nonlinear Dynam. Oct 2023, 18(10): 104501 https://doi.org/10.1115/1.4063222 The industry and the scientific community have shown interest in SCARA (Selective Compliance Assembly Robot Arm) robots due to their high accuracy. In this paper, a two-link SCARA has its end-effector pulled by three cables that generate a triangular-shaped workspace. Moving the end-effector in this region is a relatively straightforward task, but placing the end-effector outside it requires a nonlinear dynamic model and a state-of-the-art controller. To address this problem in a simpler, more efficient and innovative manner, the equations of motion are derived and three reinforcement learning algorithms are employed: Proximal Policy Optimization (the same used by the chatbot ChatGPT), Soft Actor-Critic and Twin Delayed Deep Deterministic Policy Gradient. Three targets outside the triangular workspace are considered and the trained networks have their results compared in terms of displacement error, velocity and standard deviation. The Twin Delayed Deep Deterministic Policy Gradient provides creative trajectories, the Soft Actor-Critic presents better solutions for two out of three targets, while the Proximal Policy Algorithm appears to be the most consistent considering all targets under analysis.
Back to Blog
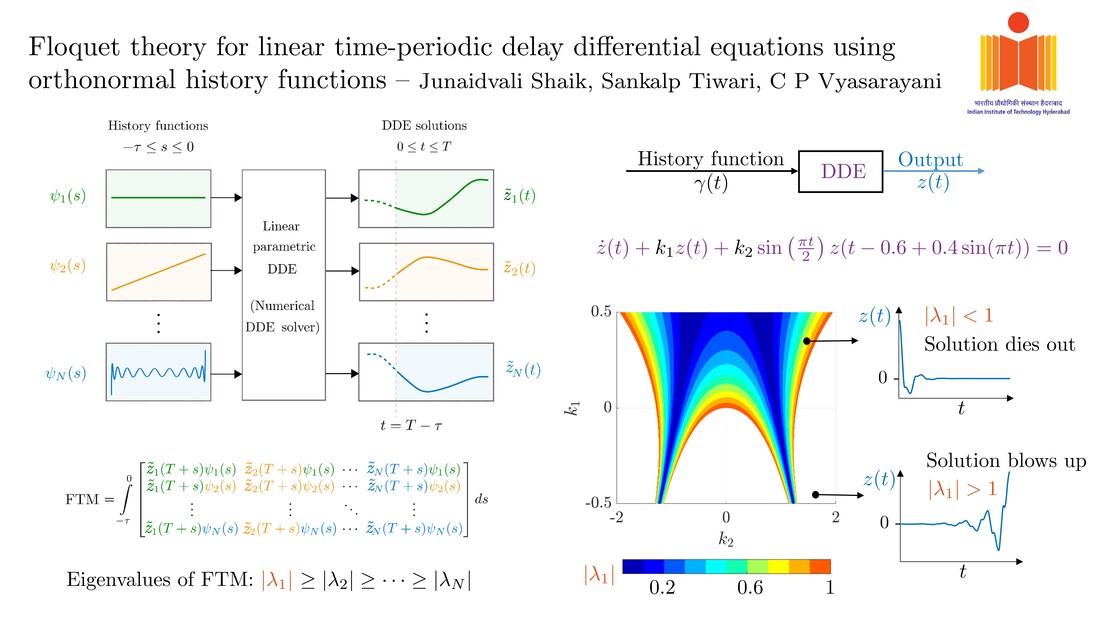
Junaidvali Shaik, Sankalp Tiwari, and C. P. Vyasarayani J. Comput. Nonlinear Dynam. Sep 2023, 18(9): 091005, https://doi.org/10.1115/1.4062633 Delayed systems are those in which the present dynamics is governed by what happened in the past. They are encountered in manufacturing, biology, population dynamics, control systems, etc. Determining linear stability of such systems is an important and difficult problem. In this work, we propose a new method to determine stability of time-periodic delay differential equations (DDEs). In the usual approaches, the DDE is converted into an approximate system of time-periodic ordinary differential equations (ODEs). Later, standard ODE techniques are employed. In this paper, we develop a method that is more direct and general. Our approach is analogous to the well-known Floquet theory for ODEs: we consider one polynomial basis function at a time as the input function and stack the coefficients of the corresponding DDE solutions to construct a matrix whose largest magnitude eigenvalue determines linear stability. We demonstrate the correctness, efficacy and convergence of our method by studying several candidate DDEs with time-periodic parameters and/or delays, and comparing the results with those obtained from other standard methods. Our approach has the following additional advantages: (a) it is parallelizable, (b) it converges quickly, and (c) it requires knowledge of only elementary linear algebra and numerical computation of DDE solutions.
Back to Blog
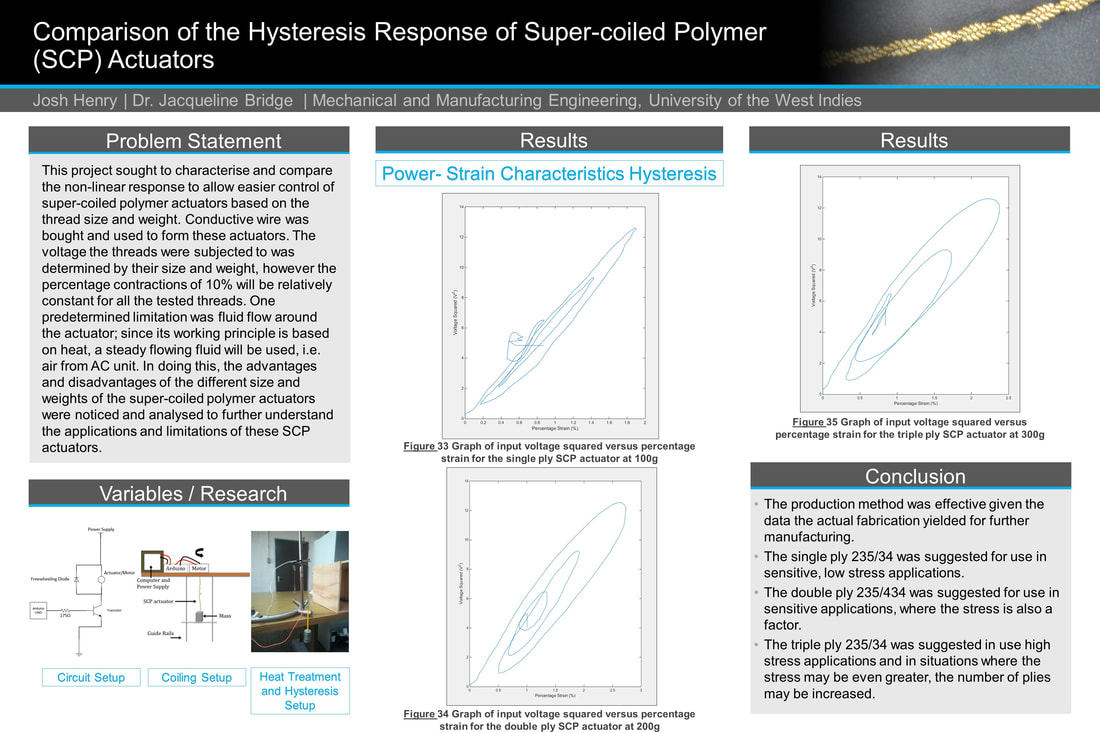
Josh H. P. Henry and Jacqueline Bridge ASME. J. Comput. Nonlinear Dynam. August 2023; 18(8): 081012. https://doi.org/10.1115/1.4062660 A major issue with advancing prosthetics and robotics technology is mimicking natural motion. Super-Coiled Polymer (SCP) actuators are an economical and high-yield alternative to traditional actuators. However, the challenge lies in identifying suitable applications due to their hysteresis. By comparing SCP actuators with varying thread sizes, this paper suggests potential directions for their utilization. The actuators were created using coiling and heat training, controlled by Arduino. MATLAB was used to analyze the recorded data, focusing on the motion to assess the hysteresis characteristics. The observed characteristics inform recommendations for diverse applications in sensitive and coarse control systems.
Back to Blog
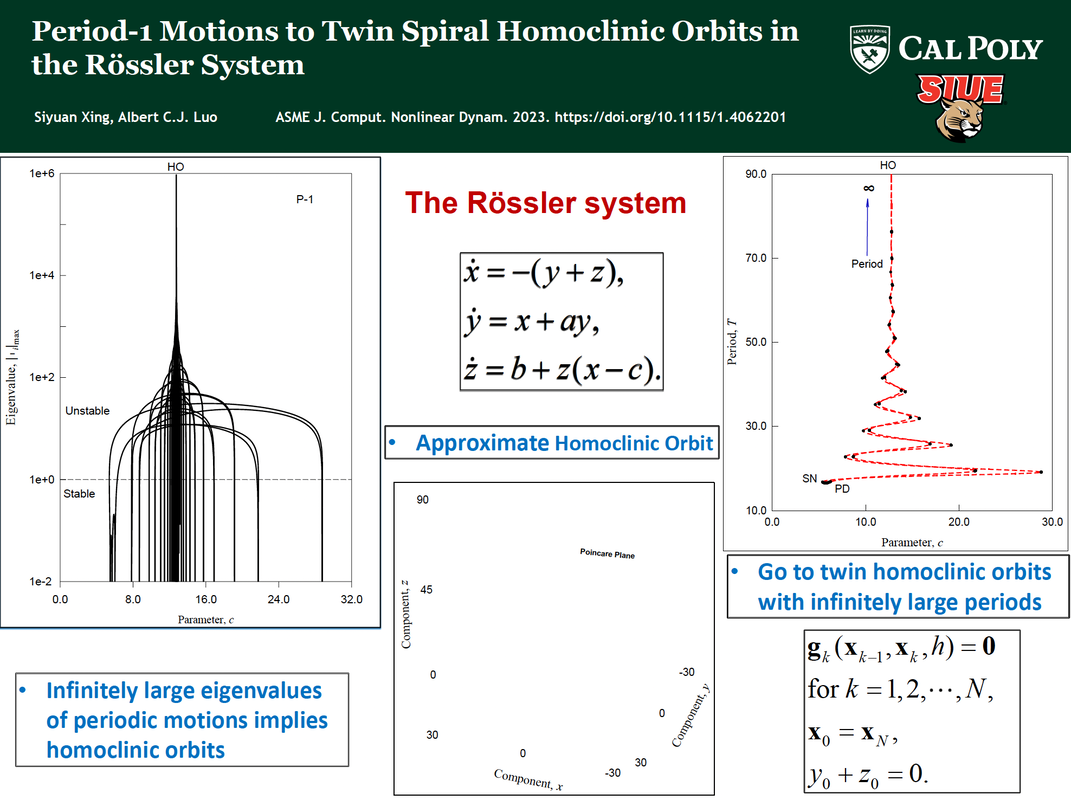
Siyuan Xing and Albert C. J. Luo, Period-1 Motions to Twin Spiral Homoclinic Orbits in the Rössler System, J. Comput. Nonlinear Dynam. Aug 2023, 18(8): 081008. https://doi.org/10.1115/1.4062201 The Rössler system was proposed as one of the simplest three-dimensional nonlinear systems in order to exhibit chaotic behaviors in 1976. Since then, extensive qualitative and quantitative research on such a system has been conducted to study the mathematical structures of periodic orbits in the vicinity of homoclinic orbits. Many advances in this field have been achieved through the linearized, approximate theory and numerical studies, but it is still far away to completely solve the problem. In this paper, the periodic motions of the Rössler system are predicted through an implicit mapping method, and the corresponding stability of periodic motions is determined by eigenvalue analysis. The semi-analytical bifurcation tree from periodic motions to two spiral homoclinic orbits is obtained. The unstable periodic motions with fast-slow movements are accurately predicted. Homoclinic orbits are identified through infinitely large eigenvalues. The approximate homoclinic orbits with different periods are presented for a better understanding of the spiral homoclinic orbits spiraling out from the saddle-focus equilibriums.
Back to Blog
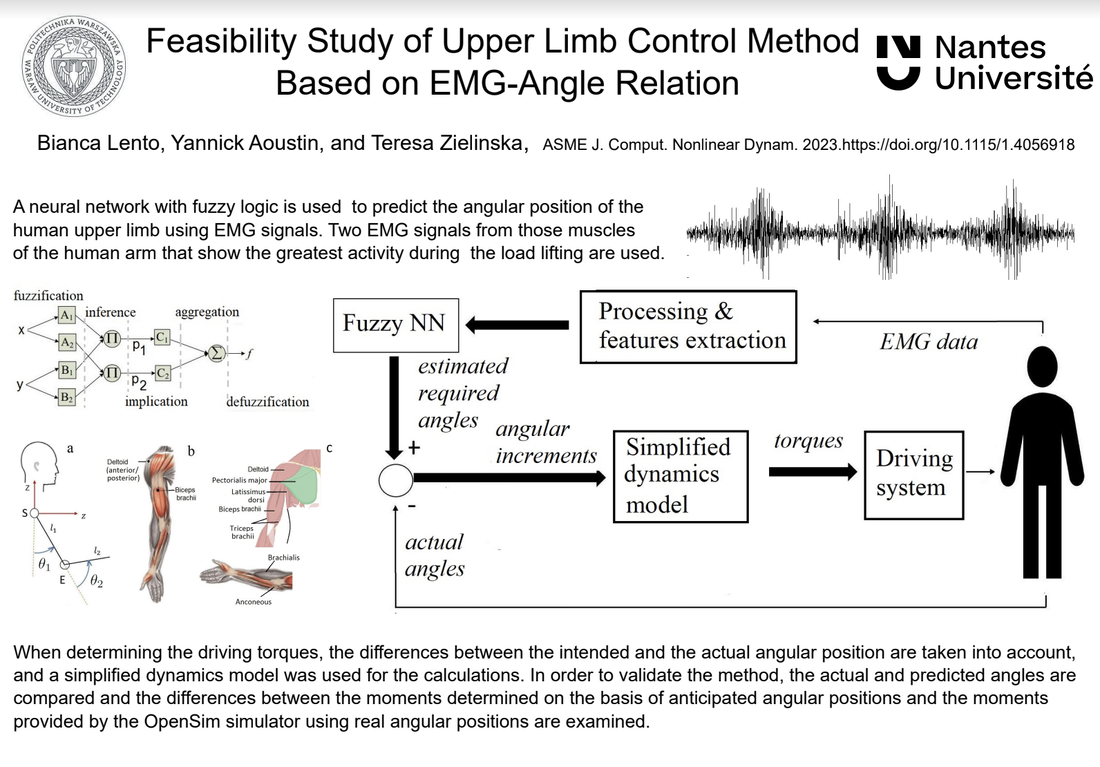
Bianca Lento, Yannick Aoustin, and Teresa Zielinska, "Feasibility Study of Upper Limb Control Method Based on EMG-Angle Relation," ASME J. Comput. Nonlinear Dynam. Jun 2023, 18(6): 064501. https://doi.org/10.1115/1.4056918 Abstract: The method of inferring the human upper limb angles basis on EMG signals with the use of fuzzy logic neural network is discussed. The planar motion in sagittal plane is taken into account, and two EMG signals are analyzed. An artificial neural network with fuzzy logic is used to process EMG signals. The network predicts angular trajectories. On the basis of the difference between the current and the intended angular position, the driving torques are determined using simplified dynamic model. To verify the method, the real and predicted angles are compared. The difference between the torques evaluated using predicted angular trajectories and simplified dynamics, and the torques delivered by the OpenSim simulator using the true data is also studied. Obtained results confirm the correctness of the concept and its usefulness for controlling prostheses or exoskeletons.
Back to Blog
Qing Wu, Xiaohua Ge, Esteban Bernal, and Pengfei Liu, "A Real-Time Fluid Dynamic Air Brake Model for Long Heavy Haul Trains," ASME J. Comput. Nonlinear Dynam. Mar 2023, 18(3): 034502 https://doi.org/10.1115/1.4056849 Practical real-time fluid dynamic air brake models for long heavy haul trains have not been reported in open literature. Based on a previous work titled ‘Railway Air Brake Model and Parallel Computing Scheme’ in the same journal, this paper proposed upgrades to the previous model and achieved the real-time feature. The real-time contributing factors included a new brake cylinder model, a new scheme for updating characteristics, and the application of parallel computing. Results show that, for a 150-wagon train emergency brake simulation, the computing speed was improved from 5.26 times slower than real-time to 8.6 times faster than real-time. The three contributions improved the computing speed by 8.8, 1.8 and 2.9 times faster than the baseline models, respectively.
Back to Blog
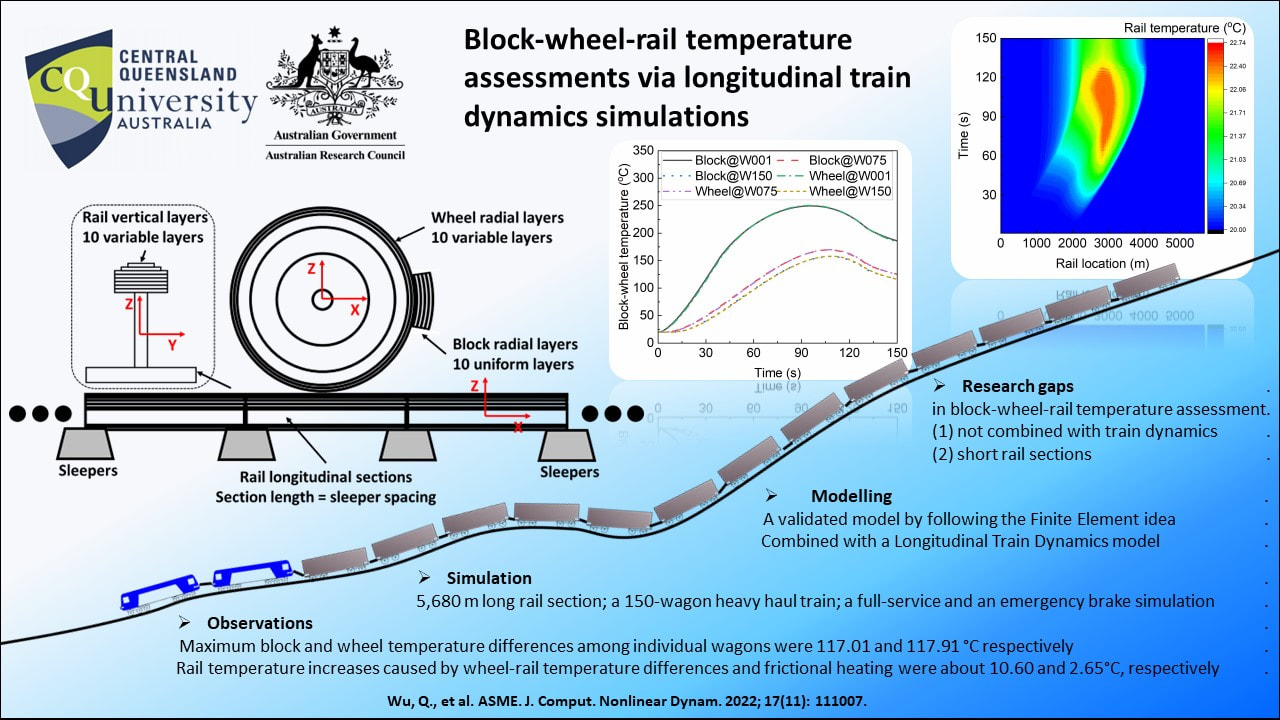
Wu, Q., Spiryagin, M., and Cole, C. (September 16, 2022). "Block–Wheel–Rail Temperature Assessments Via Longitudinal Train Dynamics Simulations." ASME. J. Comput. Nonlinear Dynam. November 2022; 17(11): 111007. https://doi.org/10.1115/1.4055431 Two research gaps were identified in block-wheel-rail temperature assessment. First, current studies are not combined with train dynamics which are better descriptions of the block-wheel-rail working environment. Second, current studies cannot simulate long rail sections. This paper developed a block-wheel-rail temperature assessment model by following the Finite Element idea. Models were validated by comparing with ANSYS Finite Element models and measured data. Case studies were carried out by combining the temperature model with a Longitudinal Train Dynamics model. A full-service and an emergency brake simulation were carried out for a 150-wagon heavy haul train on a 5,680 m long rail section. The results show that, due to brake force differences at different wagon positions, the maximum block and wheel temperature differences among individual wagons in the full-service brake simulation were 117.01 and 117.91 °C respectively. This highlighted the contribution of introducing train dynamics into block-wheel-rail temperature assessment. Rail temperature increases caused by wheel-rail temperature differences and frictional heating were about 10.60 and 2.65°C, respectively.
Back to Blog
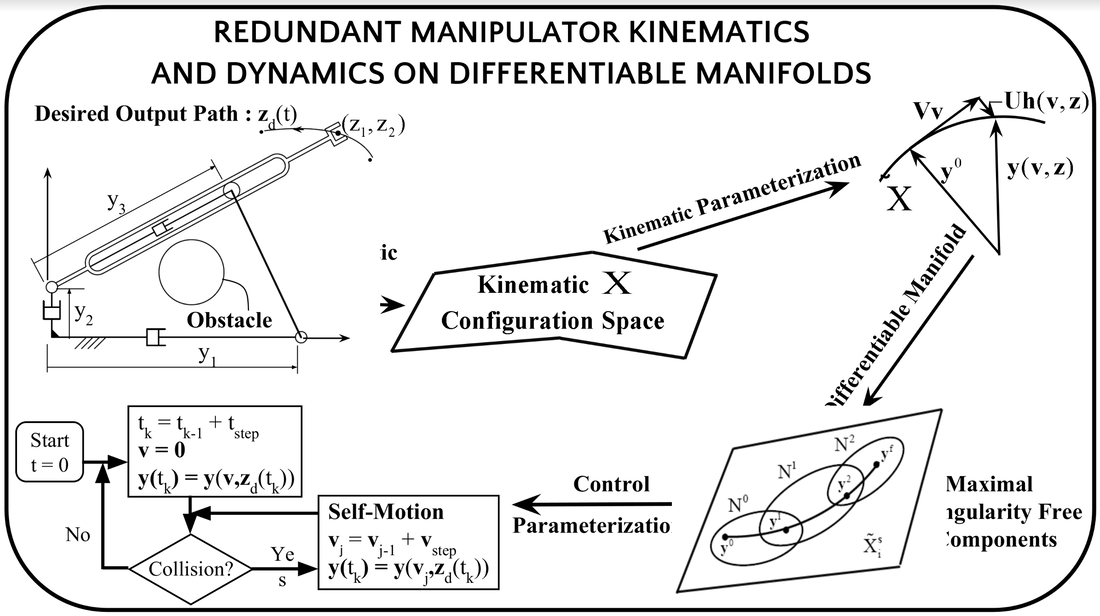
Edward J. Haug and Adrian Peidro, "Redundant Manipulator Kinematics and Dynamics on Differentiable Manifolds," ASME. J. Comput. Nonlinear Dynam. November 2022; 17(11): 111008. https://doi.org/10.1115/1.4055313 Redundant manipulators provide versatility and enhance performance potential by using a greater number of inputs than outputs to be controlled. This flexibility enables obstacle avoidance and performance optimization, in addition to achieving specified outputs. However, this requires new analytical and computational tools that enable control strategies that select from an infinite number of admissible inputs that yield the specified output, while realizing enhanced manipulator performance. Topological attributes of Euclidean space, in which manipulators function, are employed to create a differentiable manifold structure that provides explicit parameterization of the infinite number of inputs associated with a desired output. This representation is employed to demonstrate achievement of output specifications, while avoiding obstacles in the manipulator’s workspace by switching between nominal input trajectories far from obstacles to self-motions that prevent collisions otherwise. It is also applied for mapping the self-motion manifold of a seven degree of freedom robot arm that is impossible to analyze using existing methods. A time domain implementation of the parameterization is presented that provides velocity and acceleration information required for control of manipulator dynamics. Computational methods are presented that enable real-time implementation of results derived on modern high-speed microprocessors, for use in computer-based manipulator control systems.
Back to Blog
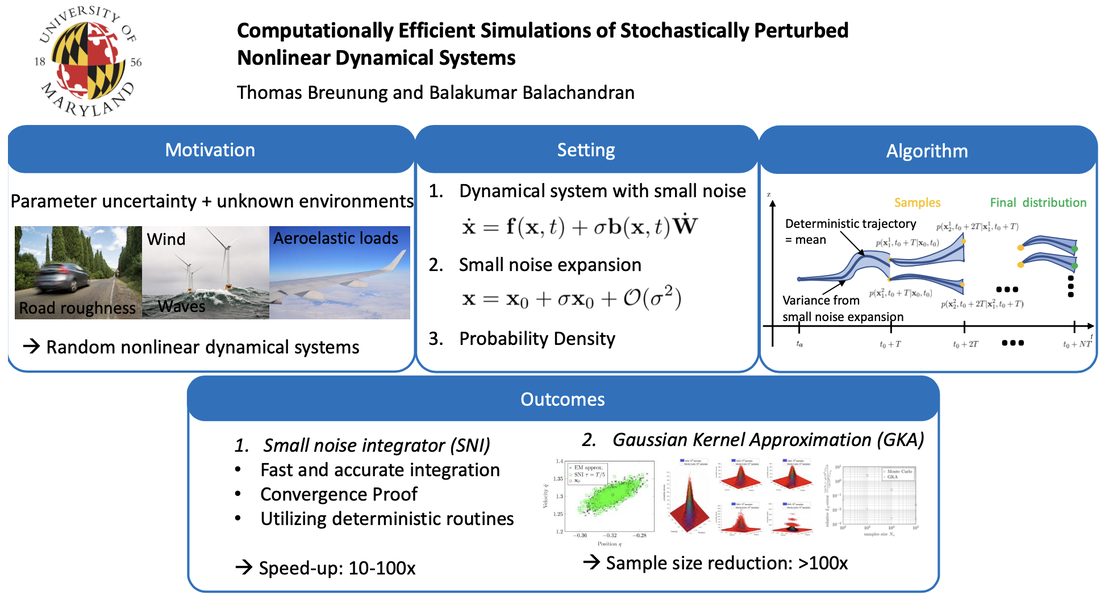
Computationally Efficient Simulations of Stochastically Perturbed Nonlinear Dynamical Systems8/2/2022 Thomas Breunung and Balakumar Balachandran, Computationally Efficient Simulations of Stochastically Perturbed Nonlinear Dynamical Systems, J. Comput. Nonlinear Dynam. Sep 2022, 17(9): 091008, https://doi.org/10.1115/1.4054932 Dynamical system models can be used to describe natural and engineering systems that evolve in time. Furthermore, most natural processes are inherently nonlinear and face uncertainties stemming from, for example, parameter variations or unknown environmental conditions. Models used to describe such systems can be grouped under stochastic, nonlinear dynamical systems. Here, the authors build on numerical integration routines meant for deterministic systems and present an algorithm to compute responses of stochastic nonlinear systems. With this approach, the well-developed deterministic tools can be used in stochastic system simulations. The algorithm’s performance is demonstrated by using numerical examples, including a system with two-hundred dimensions. This algorithm can be used to compute sample paths of stochastic dynamical systems about two orders of magnitude faster compared to established numerical stochastic integration routines. In addition, a deduced Gaussian kernel enables computations of the time-varying probability density function. With this approach, one can reduce the sample size significantly and thus enable computational investigations of higher dimensional systems that are infeasible with currently available methods. The algorithm discussed here can be used as a basis for computationally efficient investigations into stochastic dynamical systems over long time spans.
Back to Blog
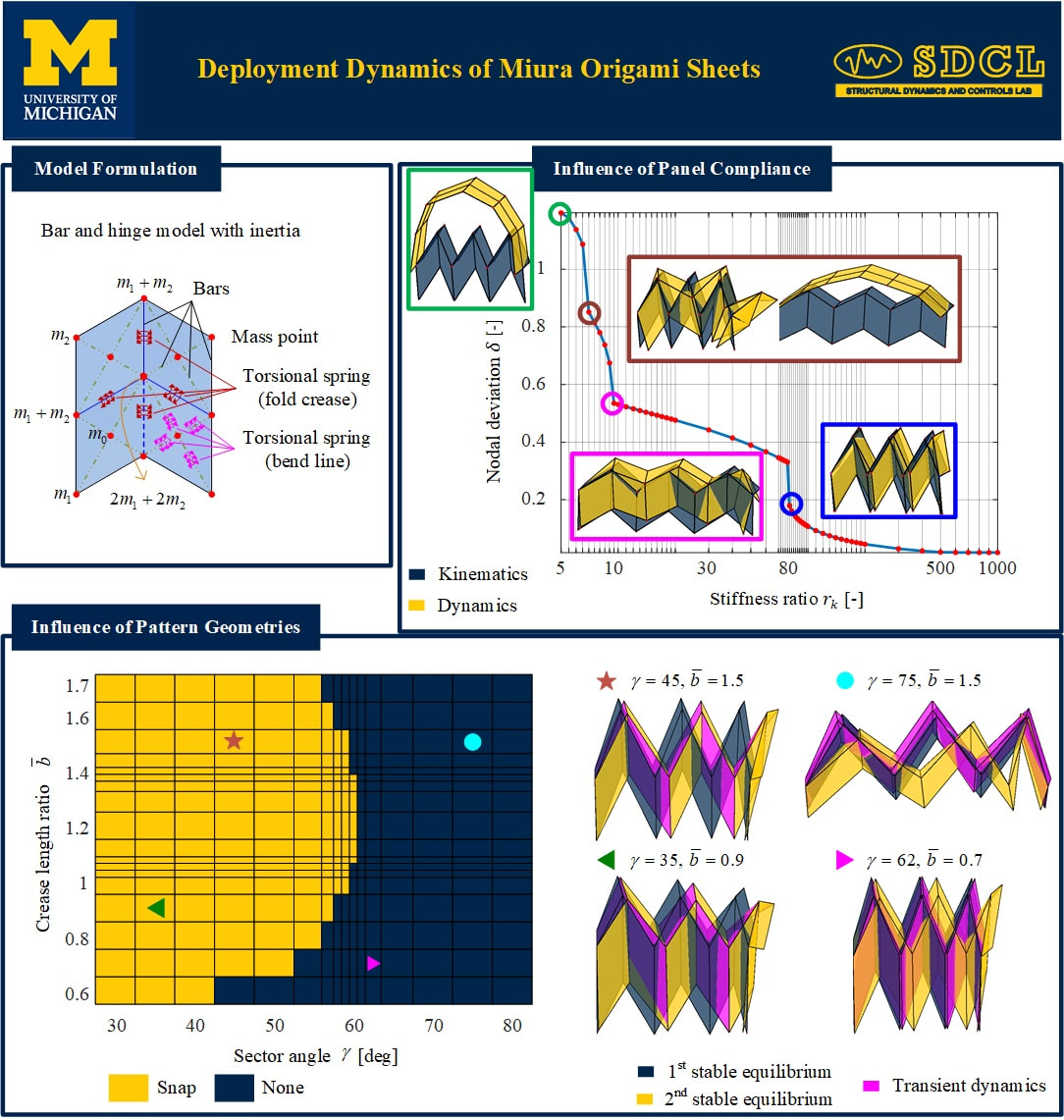
Yutong Xia, Narayanan Kidambi, Evgueni Filipov, K. W. Wang, "Deployment Dynamics of Miura Origami Sheets" ASME. J. Comput. Nonlinear Dynam. Jul 2022, 17(7): 071005. https://doi.org/10.1115/1.4054109 Origami is an ancient paper-folding art that can transform a two-dimensional (2-D) sheet into a complex 3-D structure. It has emerged as a promising tool for the design of mechanical structures with various functionalities. Because origami principles are scale independent, they can be adopted for the designs from large-scale space structures such as origami-based inflatable boom and antenna, to mesoscale origami robots, and to micro-scale medical devices. The foldability property allows for easy fabrication, compact storage, and easy transportation because origami can be compactly folded into small volumes and then unfolded to become large systems. Most studies have focused on static or kinematic deployment process of origami structures, while it is important to understand the deployment dynamics to achieve desired performances and mitigate safety concerns. In this research, we construct a dynamic model of a Miura origami sheet that captures the combined panel inertial and flexibility effects, which are otherwise ignored in rigid folding kinematic models but are critical in describing the dynamics of origami deployment. Results show that by considering these effects, the dynamic deployment behavior would substantially deviate from a nominal kinematic unfolding path. Additionally, the pattern geometries influence the effective structural stiffness, and it is shown that subtle changes can result in qualitatively different dynamic deployment behaviors. These differences are due to the multistability of the Miura origami sheet, where the structure may snap between its stable equilibria during the transient deployment process. Lastly, we show that varying the deployment rate can affect the dynamic deployment configuration. These observations are original and these phenomena have not and cannot be derived using traditional approaches. The tools and outcomes developed from this research enable a deeper understanding of the physics behind origami deployment that will pave the way for better designs of origami-based deployable structures, as well as extend our fundamental knowledge and expand our comfort zone beyond current practice.
Back to Blog
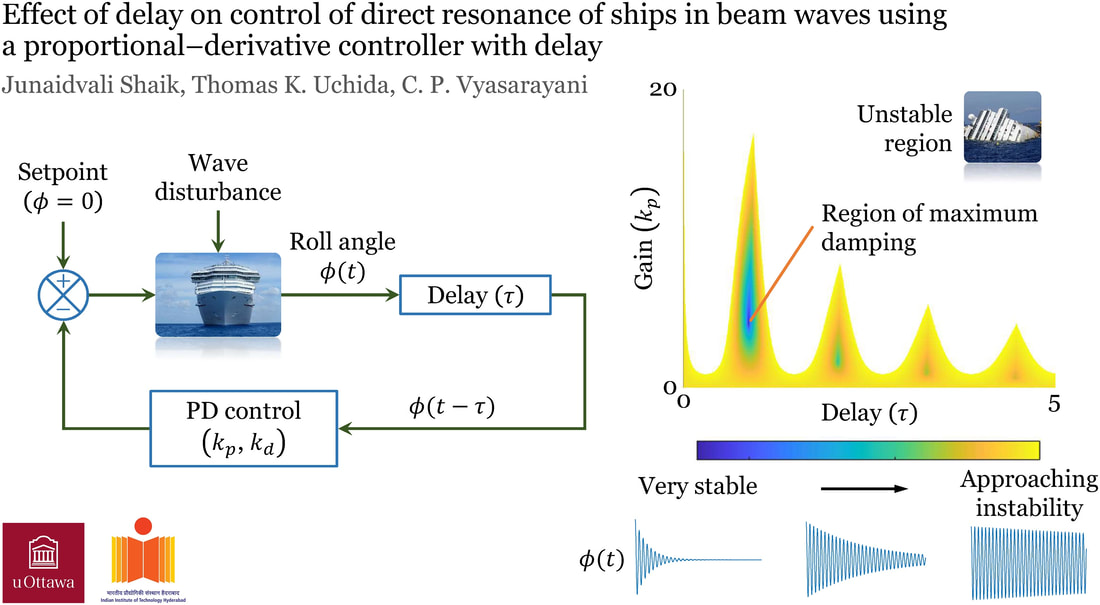
Junaidvali Shaik, Thomas K. Uchida, and C. P. Vyasarayani ASME. J. Comput. Nonlinear Dynam. June 2022; 17(6): 061004. https://doi.org/10.1115/1.4053561 Ships navigating heavy seas are susceptible to various types of wave excitation, which may lead to dynamic instabilities and, in the worst case, capsizing. Compared to the pitch and yaw motions, the roll motion of a ship has the least amount of damping. We study a harmonically excited, single-degree-of-freedom time-delay system with cubic and quintic nonlinearities. This system describes the direct resonance of a ship with an actively controlled anti-roll tank (ART) that is subjected to beam waves, or waves that are approximately perpendicular to the ship’s heading. A proportional–derivative (PD) controller with a constant time delay is assumed to operate the pump in the active ART system. A key result is obtained by deriving the stability boundary of the system, in the parametric space of the control gain and the delay, from the characteristic equation of the linearized system. As shown here, a smaller controller delay is not always better since, in some cases, reducing the delay will reduce the maximum controller gain for which the system is stable. We conduct further analyses using the spectral Tau method, the method of multiple scales, the method of harmonic balance, continuation techniques, and direct numerical simulation.
Back to Blog
Harry Dankowicz, Yuqing Wang, Frank Schilder, and Michael E. Henderson (March 18, 2020). "Multidimensional Manifold Continuation for Adaptive Boundary-Value Problems." ASME. J. Comput. Nonlinear Dynam. May 2020; 15(5): 051002. https://doi.org/10.1115/1.4046498 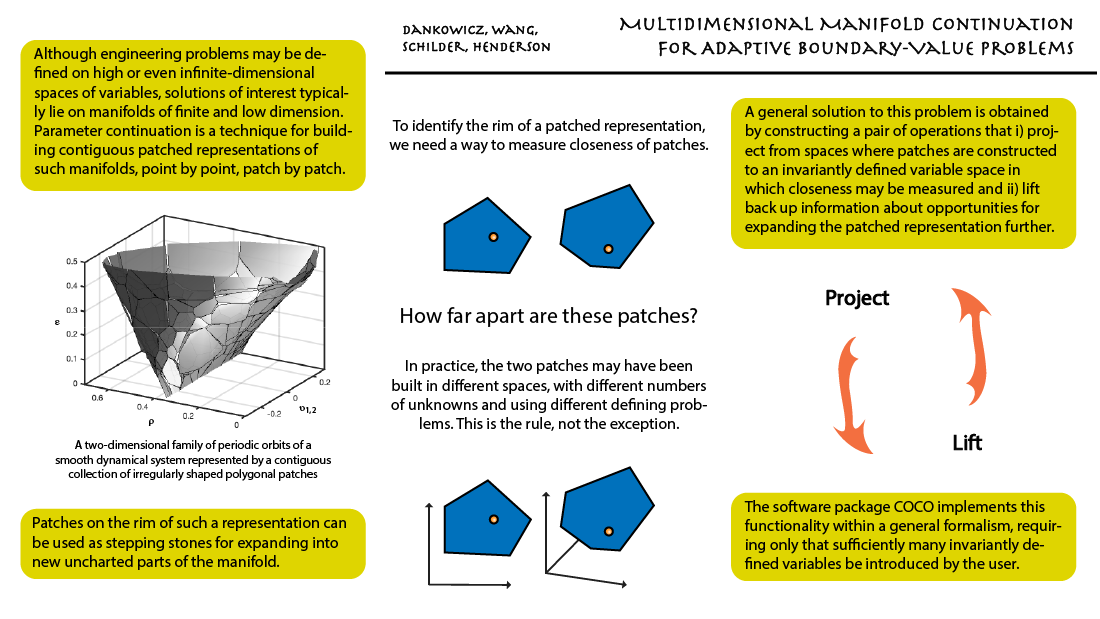 Problems of engineering analysis are often formulated as systems of nonlinear equations that impose dependencies among the unknown variables. Even as the numbers of unknowns and equations may be very large, or even infinite, the number of degrees of freedom is typically finite and small. This is true of boundary-value problems corresponding to periodic orbits of smooth dynamical systems. Here, the number of degrees of freedom equals the number of system parameters, even though the space of unknown variables is infinite-dimensional. It is rarely possible to describe all solutions of a system of nonlinear equations in terms of a single set of independent variables, equal in number to the number of degrees of freedom. It is, however, typically possible to construct a marginally larger set of dependent variables that accomplishes this goal. Such a single set of variables may also be used to describe and compare approximate solutions to an infinite-dimensional problem obtained using different discretizations or different parameterizations of the governing equations. This idea is implemented in the most recent release of the software package COCO, a parameter continuation tool for approximating finite-dimensional manifolds of solutions to nonlinear equations by successively expanding piecewise-flat covers of such manifolds. Uniquely to this tool, analysis can proceed even when the problem discretization and parameterization vary during continuation, for example, when adapting a mesh to accommodate constraints on estimated discretization errors. As demonstrated in this paper, orders of magnitude reductions in computational costs result from judicious variable choices and degeneracies associated with phase invariances, as occur for periodic response of autonomous systems, can be eliminated with or without additional phase conditions. |
 RSS Feed
RSS Feed