Archives
February 2024
Categories
All
|
Back to Blog
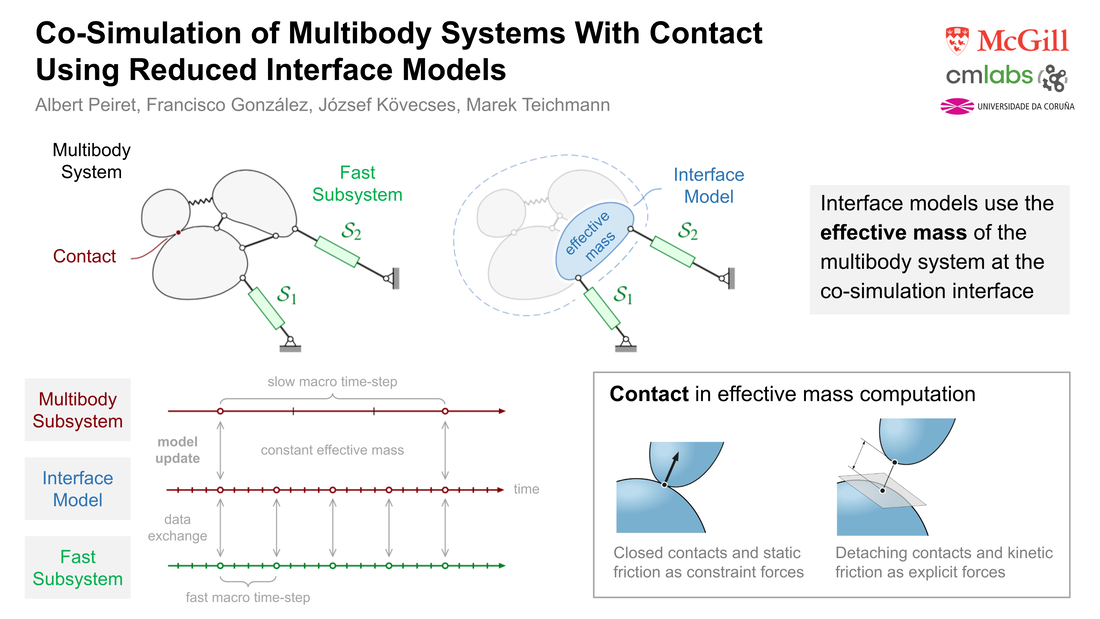
Albert Peiret, Francisco González, József Kövecses, and Marek Teichmann (February 24, 2020). "Co-Simulation of Multibody Systems With Contact Using Reduced Interface Models." ASME. J. Comput. Nonlinear Dynam. April 2020; 15(4): 041001. https://doi.org/10.1115/1.4046052 Co-simulation techniques enable the coupling of models of physically diverse subsystems in an efficient and modular way. Communication between subsystems takes place at discrete time points and is limited to a given set of coupling variables, while the internal details of the subsystems remain undisclosed, and are generally not accessible to the rest of the simulation environment. This can lead to the instability in non-iterative co-simulation that is commonly used in real-time applications. The stability of the simulation in these cases can be enhanced using reduced, effective models of one or more subsystems. These reduced models provide physically meaningful information to the other subsystems between communication points. This work describes such interface models and their application in co-simulation for nonsmooth mechanical systems subjected to unilateral contact and friction. The performance of the proposed approach is shown in some challenging examples of non-iterative, multirate co-simulation interfacing mechanical and hydraulic subsystems. The use of an interface model improves stability and allows for larger integration step-sizes, thus resulting in more efficient simulation.
0 Comments
Read More
Back to Blog
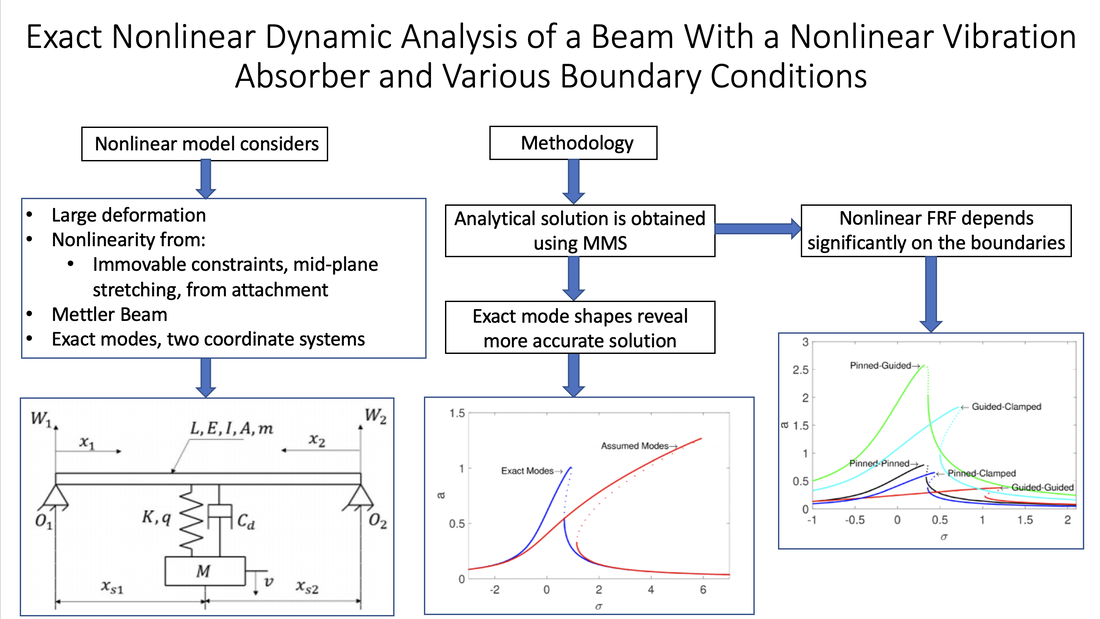
Mohammad Bukhari and Oumar Barry (November 11, 2019). "Exact Nonlinear Dynamic Analysis of a Beam With a Nonlinear Vibration Absorber and With Various Boundary Conditions." ASME. J. Comput. Nonlinear Dynam. January 2020; 15(1): 011003. https://doi.org/10.1115/1.4045287 Beams are the basic component of many engineering applications. They are used in bridges, overhead transmission lines, pipelines, sensors, aircraft structures, and many others. To ensure safety and proper function, vibrations of beams need to be investigated for better prediction of the system dynamical response. When the vibration amplitude is small, linear theory can predict the response accurately. However, when the vibration amplitude becomes larger, nonlinearity must be considered to avoid erroneous results. This work investigates the nonlinear vibration of a beam with attached Nonlinear Vibration Absorber (NVA) consisting of a spring-mass system). The considered nonlinearity stems from mid-plane stretching due to immovable boundary conditions and from the nonlinear stiffness in the NVA. In addition, different types of immovable boundary are investigated. For weak nonlinearity, an approximate analytical solution is derived using the method of multiple scales. These analytical results are validated using direct numerical integration. Parametric studies demonstrate that the performance of the NVA does not only depend on its key design variables and location, but also on the beam boundary conditions, midplane stretching of the beam, and NVA configuration (i.e., grounded versus ungrounded). Our analysis also indicates that the common approach of employing approximate modes in estimating the nonlinear response of a loaded beam produces significant error, up to 1200% in some cases. These findings could contribute to the design improvement of NVAs, microelectromechanical systems (MEMS), energy harvesters, and metastructures.
Back to Blog
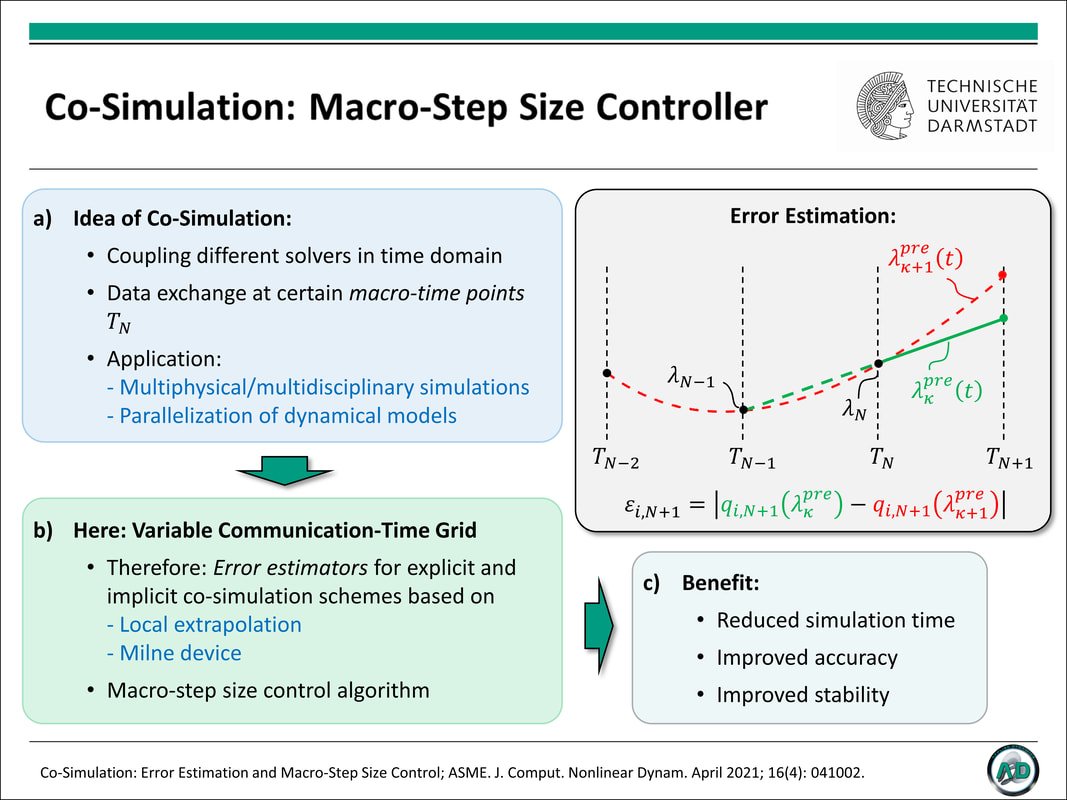
T. Meyer, J. Kraft, and B. Schweizer (February 24, 2021). "Co-Simulation: Error Estimation and Macro-Step Size Control." ASME. J. Comput. Nonlinear Dynam. April 2021; 16(4): 041002. https://doi.org/10.1115/1.4048944 Co-simulation techniques are commonly used to analyze multidisciplinary and multiphysical systems as well as to parallelize dynamical simulation models. Therefore, the overall system is decomposed into a certain number of subsystems. To define the coupling between the subsystems, coupling equations and appropriate coupling variables have to be specified. Moreover, a communication-time grid has to be introduced by defining macro-time points . The subsystems are integrated independently between the communication-time points; coupling variables are only exchanged at the macro-time points. The crucial point in connection with equidistant communication-time grids, which are frequently used in practical applications, is the appropriate choice of the macro-step size. Efficiency and accuracy of a co-simulation may, however, considerably be increased by using a variable communication-time grid. Therefore, an error estimator for controlling the macro-step size is required. Here, different error estimators for explicit and implicit co-simulation schemes are derived and incorporated into the macro-step size control algorithm. Numerical studies clearly demonstrate that the main problems associated with equidistant macro-grids – namely a trade-off between stability/accuracy and efficiency – disappear, if variable communication-time grids are used. The manuscript focuses on mechanical co-simulation models. The basic results may, however, also be applied to arbitrary, non-mechanical co-simulation models.
Back to Blog
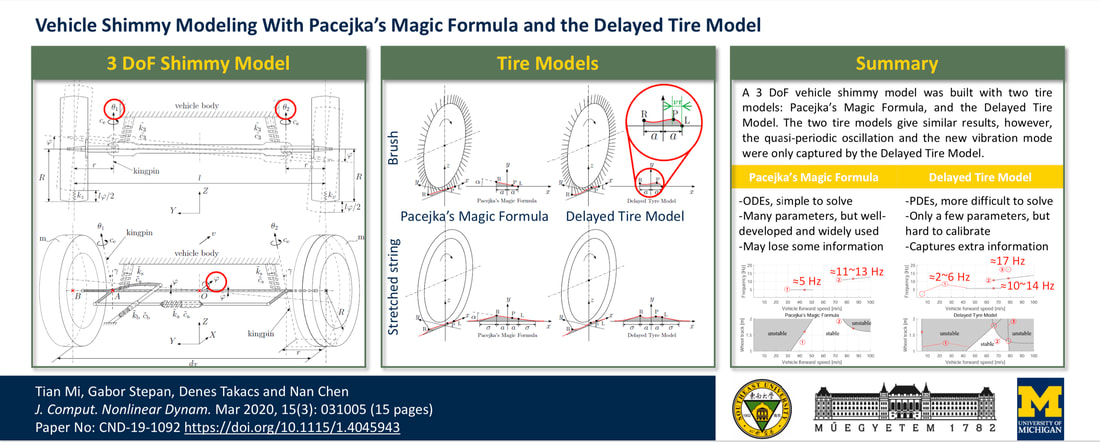
Tian Mi, Gabor Stepan, Denes Takacs, and Nan Chen (January 23, 2020). "Vehicle Shimmy Modeling With Pacejka's Magic Formula and the Delayed Tire Model." ASME. J. Comput. Nonlinear Dynam. March 2020; 15(3): 031005. https://doi.org/10.1115/1.4045943 Shimmy is a self-excited vibration which can appear in various wheeled mechanisms such as trailers, motorcycles, bicycles, cars, landing gears of aircrafts, and even baby strollers or supermarket trolleys. Shimmy of cars is also known as vehicle shimmy or death wobble. The cause of shimmy is related to the dynamic characteristics of the tire-road contact and the overall system structure. It increases tire wear, deteriorates vehicle handling, and causes further instability problems of the whole vehicle. In this paper, a 3 degree-of-freedom model of vehicle front wheels with dependent suspension is studied from the viewpoint of possible appearance of shimmy, and two tire models are compared. The two tire models have essentially different assumptions: Pacejka’s magic formula uses linearization in space along the tire-ground contact line where the tire points stick to the ground, while the delayed tire model uses linearization in time by considering small (but spatially nonlinear) lateral deformations of the tire in the contact region. The theoretical results show that the delayed tire model presents additional instabilities (i.e., shimmy) at low speeds, and especially at low damping values. The investigation of this model is motivated by the occurrence of shimmy on some heavy vehicles and jeeps with worn front wheel suspension system, and the conclusions might be useful in the future study of shimmy in systems with independent suspensions of some electric vehicles.
Back to Blog
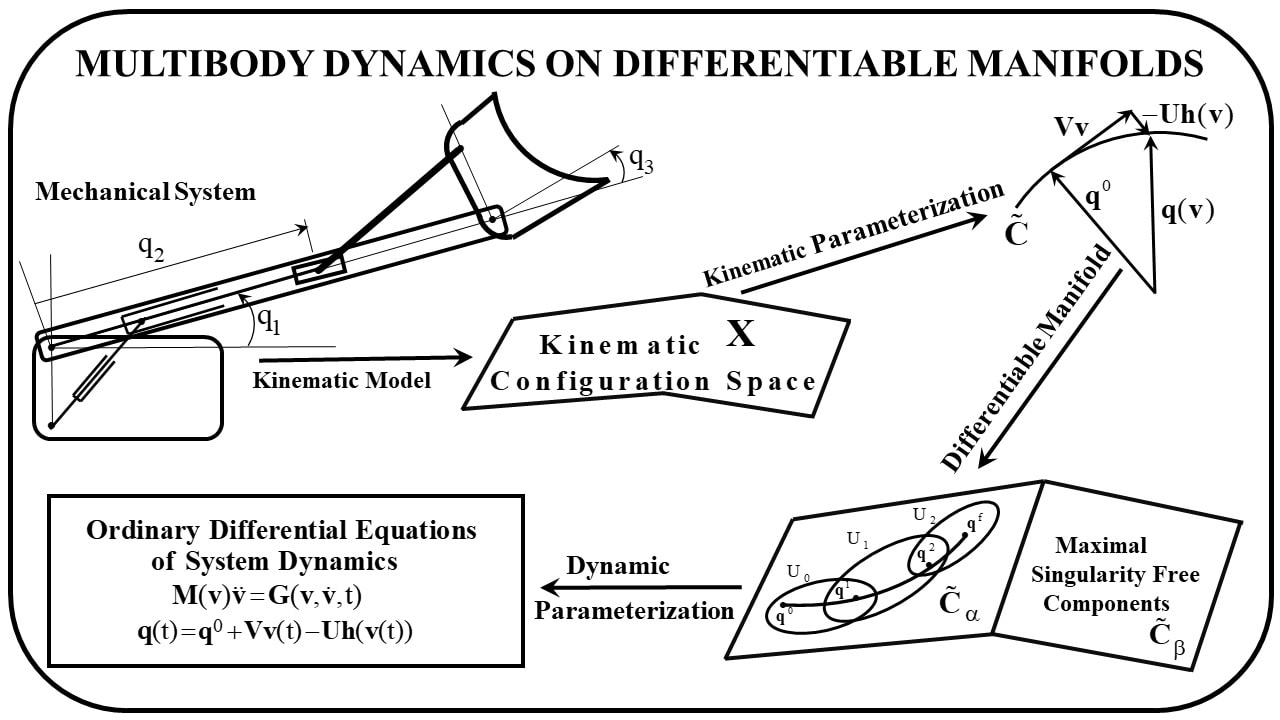
Edward J. Haug (February 24, 2021). "Multibody Dynamics on Differentiable Manifolds." ASME. J. Comput. Nonlinear Dynam. April 2021; 16(4): 041003. https://doi.org/10.1115/1.4049995
Topological and vector space attributes of Euclidean space are consolidated from the mathematical literature and employed to create a differentiable manifold structure for multibody kinematics and dynamics. A kinematic configuration space representation of admissible motion of a mechanical system provides the foundation for the development. Using vector space properties of Euclidean space and multivariable calculus, a tangent space kinematic parameterization is presented that establishes the regular configuration space of a multibody system as a differentiable manifold. Topological properties of Euclidean space show that this manifold is naturally partitioned into maximal, singularity free components of kinematic and dynamic functionality. A dynamic parameterization of the d’Alembert variational equation of multibody dynamics yields singularity free ordinary differential equations of system dynamics on these components, without introducing Lagrange multipliers. Solutions of the differential equations satisfy configuration, velocity, and acceleration constraint equations and the variational equations of dynamics; i.e., multibody kinematics and dynamics are embedded in these ordinary differential equations. Two examples, one planar and one spatial, are treated using the formulation presented. Solutions obtained are shown to satisfy all three forms of kinematic constraint to within specified error tolerances, using fourth order Runge-Kutta numerical integration methods. |
 RSS Feed
RSS Feed