Attractors’ analysis and bifurcation diagrams for an impacting inverted pendulum in the presence of a two-terms harmonic excitation

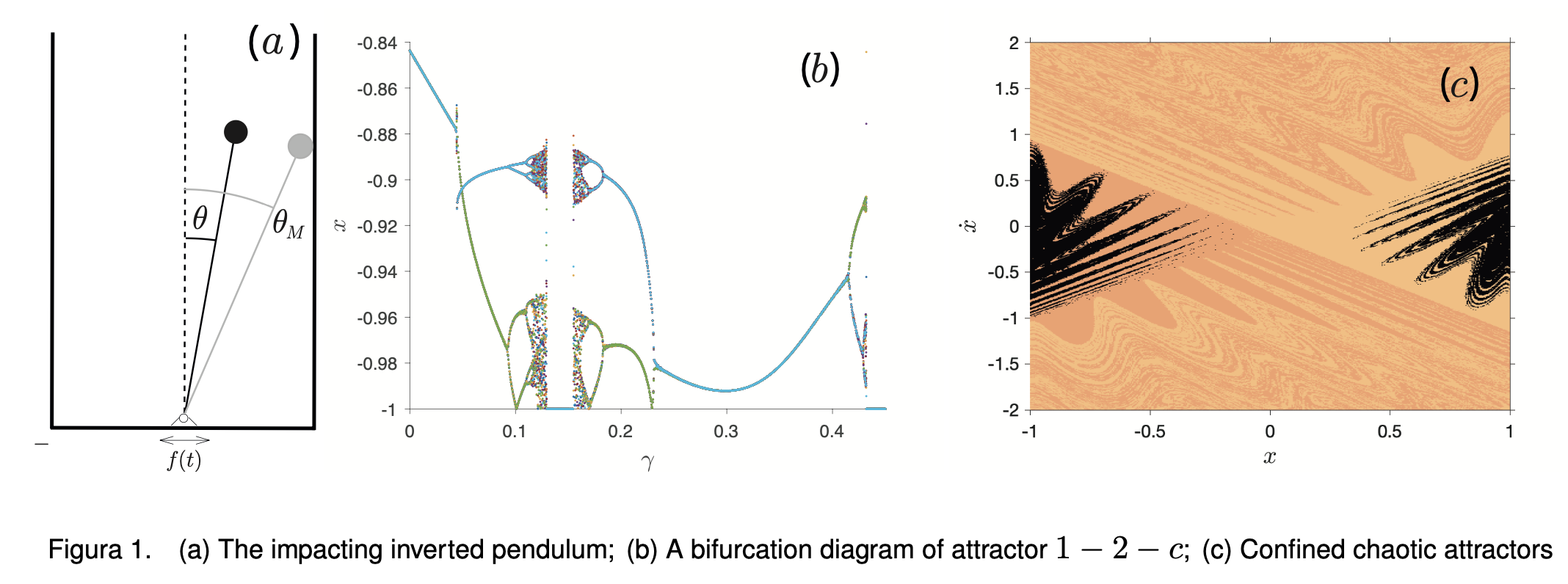
Milena Petrini, Lucio Demeio and Stefano Lenci  
ASME. J. Comput. Nonlinear Dyn. October 2023, 18(10): 101004
https://doi.org/10.1115/1.4063034 

In this work we examine the nonlinear dynamics of an inverted pendulum between lateral rebounding barriers. We continue the numerical investigation started in (Demeio et al., 2006, “Response Scenario and Non-Smooth Features in the Nonlinear Dynamics of an Impacting Inverted Pendulum”, ASME J. Comput. Nonlin. Dyn., 1(1), pp. 56-64) by adding the contribution of the second harmonic in the external forcing term. We investigate the behavior of the periodic attractors by bifurcation diagrams with respect to each amplitude and by behavior charts of single attractors in the amplitude parameters plane for fixed frequency. We study the effects of the second harmonic term on the existence domain of each attractor, on local bifurcations and on the changes in the basins of attraction. The behavior of some robust chaotic attractor is also considered. In the evolution of the periodic attractors we have observed that the addition of the second harmonic generates a rich variety of behaviors, such as loss of stability and formation of isolas of periodic orbits. In the case of chaotic attractors, we have studied one attractor at high frequency, ω = 18, and one at low frequency, ω = 3. In the high frequency case we detect a transition from a scattered to a confined attractor, whereas at the lower frequency the chaotic attractor is present over a wide range of the second harmonic’s amplitude. Finally, we extend the investigation of the chaotic attractors by bifurcation diagrams with respect to the frequency. 

Full Paper