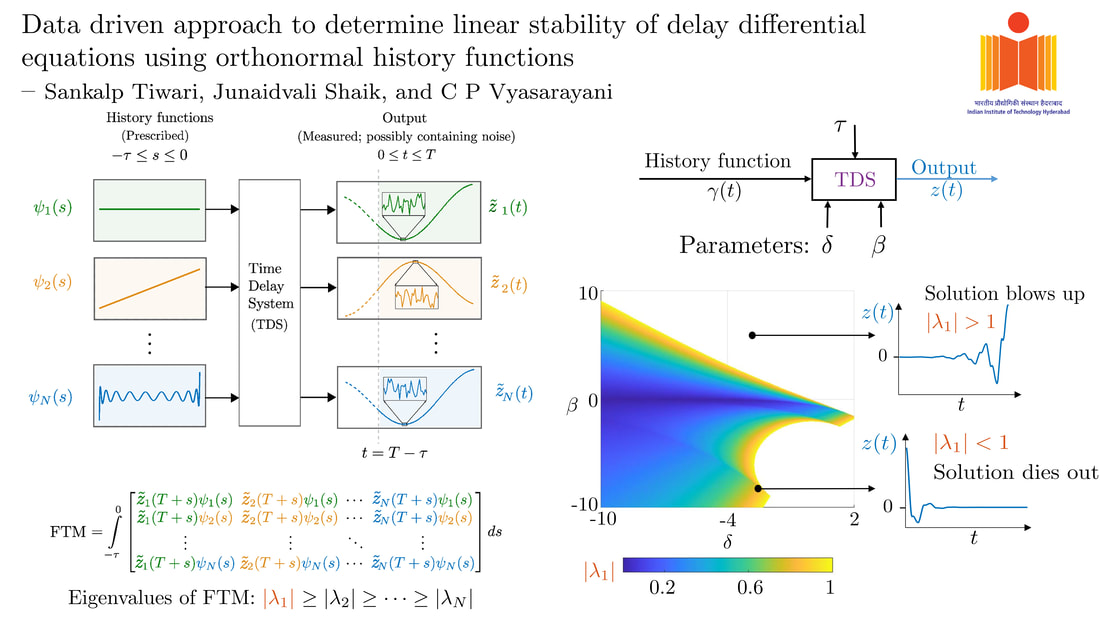
Sankalp Tiwari, Junaidvali Shaik, and C. P. Vyasarayani
J. Comput. Nonlinear Dynam. Feb 2024, 19(2): 021002 
​https://doi.org/10.1115/1.4064251

​Delayed systems are those in which the present dynamics is governed by what happened in the past. They are encountered in manufacturing, biology, population dynamics, control systems, etc. Determining stability of such systems is an important and difficult problem. In the existing works, stability is determined by assuming the governing differential equation. However, the equation may not be known or difficult to obtain. Unlike existing works, our method determines the linear stability of a delayed system using its response to a few known inputs. In particular, our method does not require or assume the differential equation governing that system. The only system information we use is its largest delay time, and the only assumption we make about the underlying equation is that its coefficients are either constant or time-periodic. Our approach involves giving the first few functions of an orthonormal polynomial basis as input and measuring/computing the corresponding responses to generate a state transition matrix, whose largest eigenvalue determines the stability. We demonstrate our method's correctness, efficacy, and convergence by studying four candidate DDEs with differing features. Importantly, we show that our approach is robust to noise in measurement, thereby establishing its suitability for practical applications.

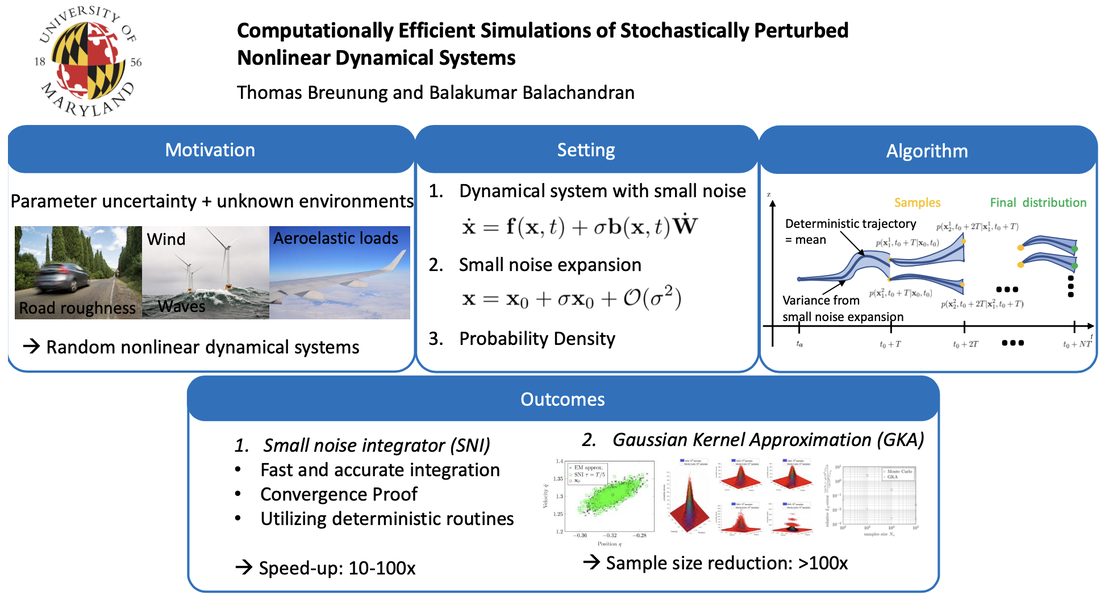
Thomas Breunung and Balakumar Balachandran, Computationally Efficient Simulations of Stochastically Perturbed Nonlinear Dynamical Systems, J. Comput. Nonlinear Dynam. Sep 2022, 17(9): 091008, https://doi.org/10.1115/1.4054932

Dynamical system models can be used to describe natural and engineering systems that evolve in time. Furthermore, most natural processes are inherently nonlinear and face uncertainties stemming from, for example, parameter variations or unknown environmental conditions. Models used to describe such systems can be grouped under stochastic, nonlinear dynamical systems. Here, the authors build on numerical integration routines meant for deterministic systems and present an algorithm to compute responses of stochastic nonlinear systems. With this approach, the well-developed deterministic tools can be used in stochastic system simulations. The algorithm’s performance is demonstrated by using numerical examples, including a system with two-hundred dimensions. This algorithm can be used to compute sample paths of stochastic dynamical systems about two orders of magnitude faster compared to established numerical stochastic integration routines. In addition, a deduced Gaussian kernel enables computations of the time-varying probability density function. With this approach, one can reduce the sample size significantly and thus enable computational investigations of higher dimensional systems that are infeasible with currently available methods. The algorithm discussed here can be used as a basis for computationally efficient investigations into stochastic dynamical systems over long time spans.