Data Driven Approach to Determine Linear Stability of Delay Differential Equations Using Orthonormal History Functions

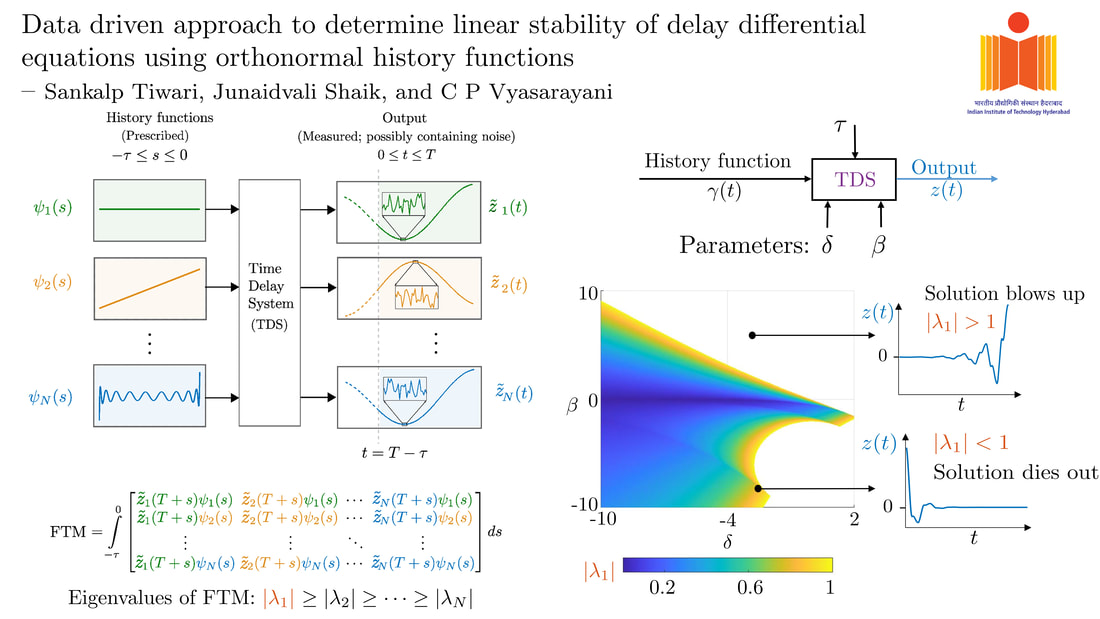
Sankalp Tiwari, Junaidvali Shaik, and C. P. Vyasarayani
J. Comput. Nonlinear Dynam. Feb 2024, 19(2): 021002 
​https://doi.org/10.1115/1.4064251

​Delayed systems are those in which the present dynamics is governed by what happened in the past. They are encountered in manufacturing, biology, population dynamics, control systems, etc. Determining stability of such systems is an important and difficult problem. In the existing works, stability is determined by assuming the governing differential equation. However, the equation may not be known or difficult to obtain. Unlike existing works, our method determines the linear stability of a delayed system using its response to a few known inputs. In particular, our method does not require or assume the differential equation governing that system. The only system information we use is its largest delay time, and the only assumption we make about the underlying equation is that its coefficients are either constant or time-periodic. Our approach involves giving the first few functions of an orthonormal polynomial basis as input and measuring/computing the corresponding responses to generate a state transition matrix, whose largest eigenvalue determines the stability. We demonstrate our method's correctness, efficacy, and convergence by studying four candidate DDEs with differing features. Importantly, we show that our approach is robust to noise in measurement, thereby establishing its suitability for practical applications.

full paper