Archives
February 2024
Categories
All
|
Back to Blog
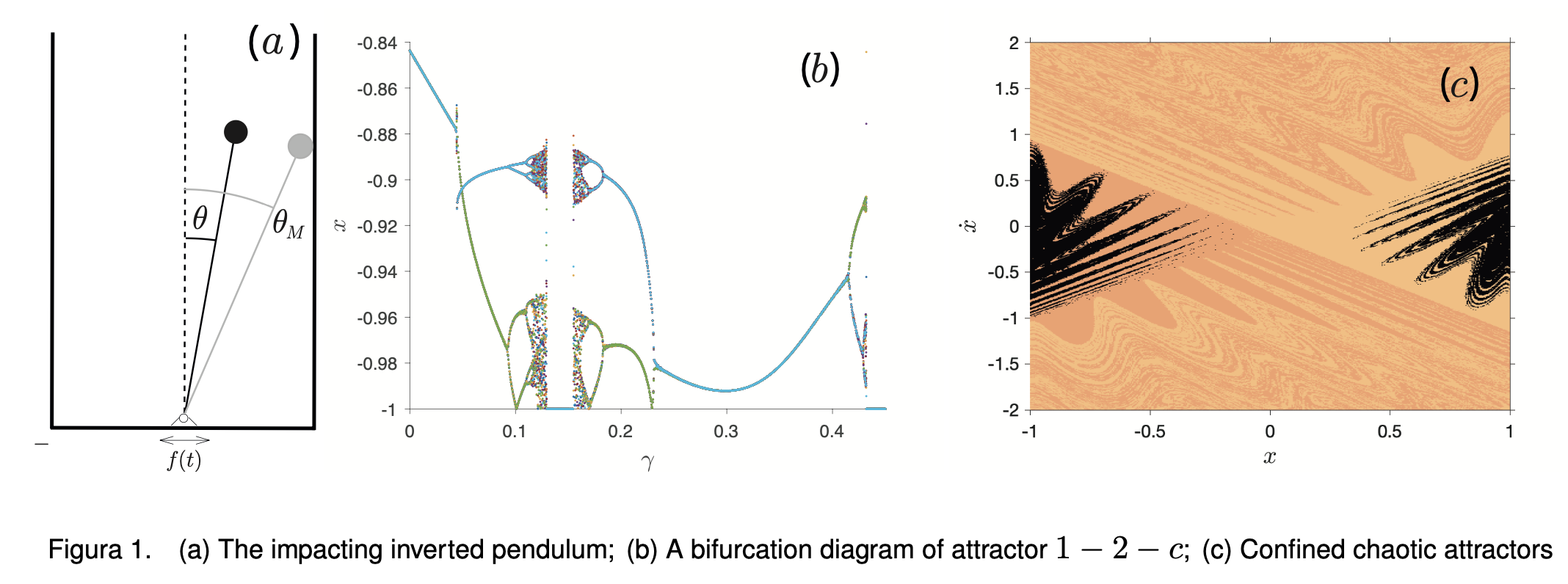
Milena Petrini, Lucio Demeio and Stefano Lenci ASME. J. Comput. Nonlinear Dyn. October 2023, 18(10): 101004 https://doi.org/10.1115/1.4063034 In this work we examine the nonlinear dynamics of an inverted pendulum between lateral rebounding barriers. We continue the numerical investigation started in (Demeio et al., 2006, “Response Scenario and Non-Smooth Features in the Nonlinear Dynamics of an Impacting Inverted Pendulum”, ASME J. Comput. Nonlin. Dyn., 1(1), pp. 56-64) by adding the contribution of the second harmonic in the external forcing term. We investigate the behavior of the periodic attractors by bifurcation diagrams with respect to each amplitude and by behavior charts of single attractors in the amplitude parameters plane for fixed frequency. We study the effects of the second harmonic term on the existence domain of each attractor, on local bifurcations and on the changes in the basins of attraction. The behavior of some robust chaotic attractor is also considered. In the evolution of the periodic attractors we have observed that the addition of the second harmonic generates a rich variety of behaviors, such as loss of stability and formation of isolas of periodic orbits. In the case of chaotic attractors, we have studied one attractor at high frequency, ω = 18, and one at low frequency, ω = 3. In the high frequency case we detect a transition from a scattered to a confined attractor, whereas at the lower frequency the chaotic attractor is present over a wide range of the second harmonic’s amplitude. Finally, we extend the investigation of the chaotic attractors by bifurcation diagrams with respect to the frequency.
0 Comments
Read More
Back to Blog
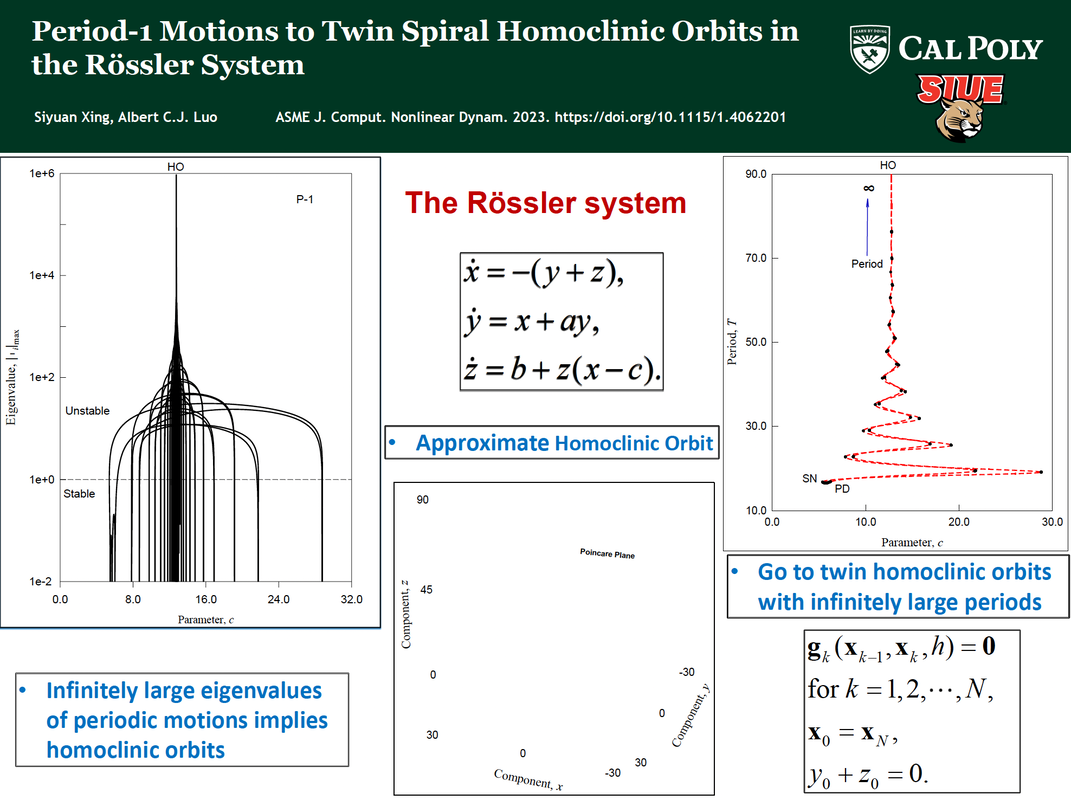
Siyuan Xing and Albert C. J. Luo, Period-1 Motions to Twin Spiral Homoclinic Orbits in the Rössler System, J. Comput. Nonlinear Dynam. Aug 2023, 18(8): 081008. https://doi.org/10.1115/1.4062201 The Rössler system was proposed as one of the simplest three-dimensional nonlinear systems in order to exhibit chaotic behaviors in 1976. Since then, extensive qualitative and quantitative research on such a system has been conducted to study the mathematical structures of periodic orbits in the vicinity of homoclinic orbits. Many advances in this field have been achieved through the linearized, approximate theory and numerical studies, but it is still far away to completely solve the problem. In this paper, the periodic motions of the Rössler system are predicted through an implicit mapping method, and the corresponding stability of periodic motions is determined by eigenvalue analysis. The semi-analytical bifurcation tree from periodic motions to two spiral homoclinic orbits is obtained. The unstable periodic motions with fast-slow movements are accurately predicted. Homoclinic orbits are identified through infinitely large eigenvalues. The approximate homoclinic orbits with different periods are presented for a better understanding of the spiral homoclinic orbits spiraling out from the saddle-focus equilibriums.
Back to Blog
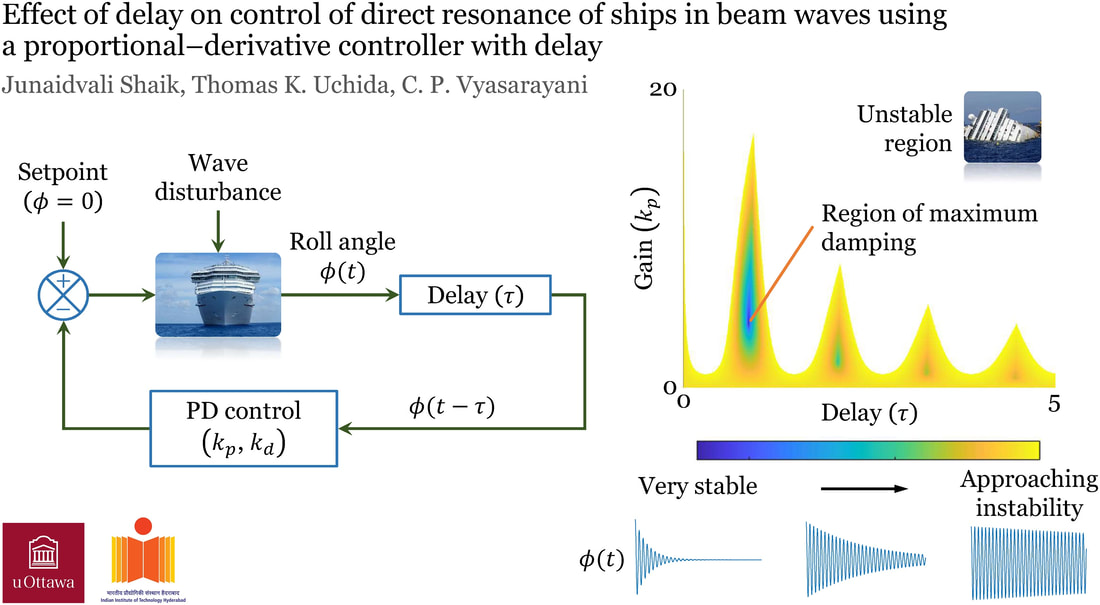
Junaidvali Shaik, Thomas K. Uchida, and C. P. Vyasarayani ASME. J. Comput. Nonlinear Dynam. June 2022; 17(6): 061004. https://doi.org/10.1115/1.4053561 Ships navigating heavy seas are susceptible to various types of wave excitation, which may lead to dynamic instabilities and, in the worst case, capsizing. Compared to the pitch and yaw motions, the roll motion of a ship has the least amount of damping. We study a harmonically excited, single-degree-of-freedom time-delay system with cubic and quintic nonlinearities. This system describes the direct resonance of a ship with an actively controlled anti-roll tank (ART) that is subjected to beam waves, or waves that are approximately perpendicular to the ship’s heading. A proportional–derivative (PD) controller with a constant time delay is assumed to operate the pump in the active ART system. A key result is obtained by deriving the stability boundary of the system, in the parametric space of the control gain and the delay, from the characteristic equation of the linearized system. As shown here, a smaller controller delay is not always better since, in some cases, reducing the delay will reduce the maximum controller gain for which the system is stable. We conduct further analyses using the spectral Tau method, the method of multiple scales, the method of harmonic balance, continuation techniques, and direct numerical simulation.
|
 RSS Feed
RSS Feed