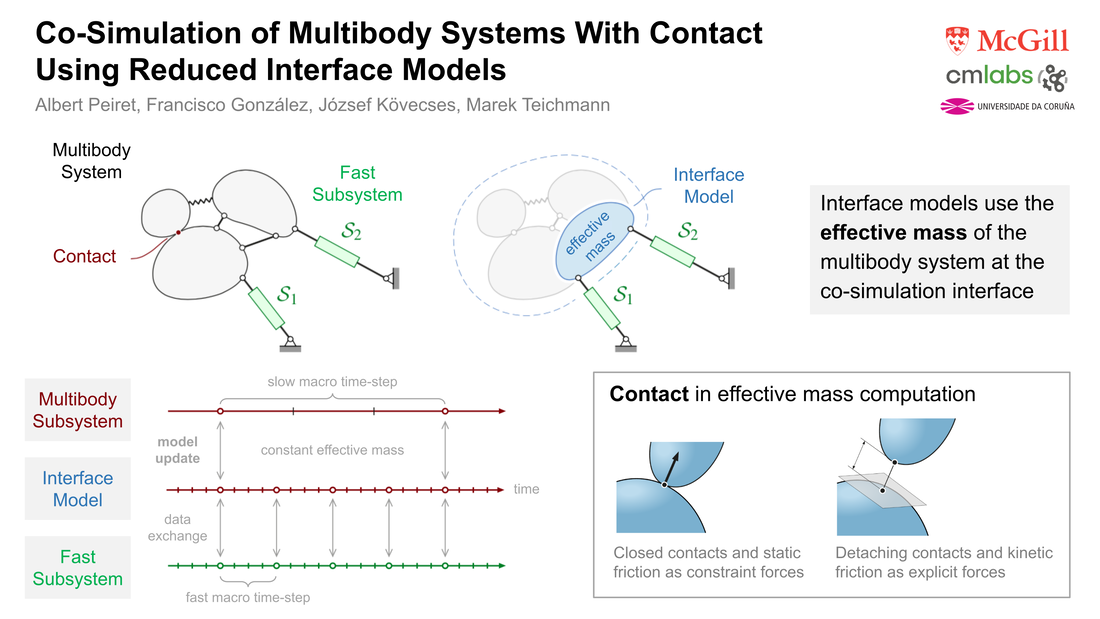
Albert Peiret, Francisco González, József Kövecses​, and Marek Teichmann (February 24, 2020). "Co-Simulation of Multibody Systems With Contact Using Reduced Interface Models." ASME. J. Comput. Nonlinear Dynam. April 2020; 15(4): 041001. https://doi.org/10.1115/1.4046052

Co-simulation techniques enable the coupling of models of physically diverse subsystems in an efficient and modular way. Communication between subsystems takes place at discrete time points and is limited to a given set of coupling variables, while the internal details of the subsystems remain undisclosed, and are generally not accessible to the rest of the simulation environment. This can lead to the instability in non-iterative co-simulation that is commonly used  in real-time applications. The stability of the simulation in these cases can be enhanced using reduced, effective models of one or more subsystems. These reduced models provide physically  meaningful information to the other subsystems between communication points.  This work describes such interface models and their application in co-simulation for nonsmooth mechanical systems subjected to unilateral contact and friction. The performance of the proposed approach is shown in some challenging examples of non-iterative, multirate co-simulation interfacing mechanical and hydraulic subsystems. The use of an interface model improves stability and allows for larger integration step-sizes, thus resulting in more efficient simulation. 

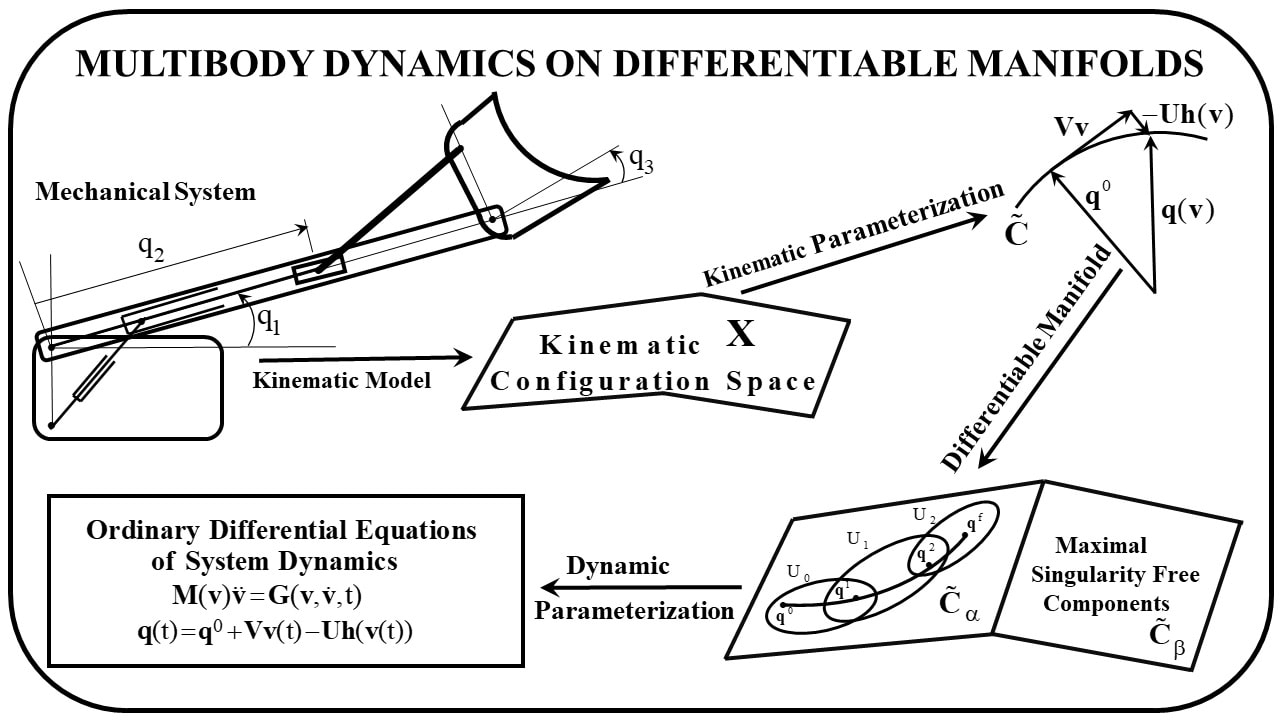
​Edward J. Haug (February 24, 2021). "Multibody Dynamics on Differentiable Manifolds." ASME. J. Comput. Nonlinear Dynam. April 2021; 16(4): 041003. https://doi.org/10.1115/1.4049995
 

​
​Topological and vector space attributes of Euclidean space are consolidated from the mathematical literature and employed to create a differentiable manifold structure for multibody kinematics and dynamics. A kinematic configuration space representation of admissible motion of a mechanical system provides the foundation for the development. Using vector space properties of Euclidean space and multivariable calculus, a tangent space kinematic parameterization is presented that establishes the regular configuration space of a multibody system as a differentiable manifold. Topological properties of Euclidean space show that this manifold is naturally partitioned into maximal, singularity free components of kinematic and dynamic functionality. A dynamic parameterization of the d’Alembert variational equation of multibody dynamics yields singularity free ordinary differential equations of system dynamics on these components, without introducing Lagrange multipliers. Solutions of the differential equations satisfy configuration, velocity, and acceleration constraint equations and the variational equations of dynamics; i.e., multibody kinematics and dynamics are embedded in these ordinary differential equations. Two examples, one planar and one spatial, are treated using the formulation presented. Solutions obtained are shown to satisfy all three forms of kinematic constraint to within specified error tolerances, using fourth order Runge-Kutta numerical integration methods.