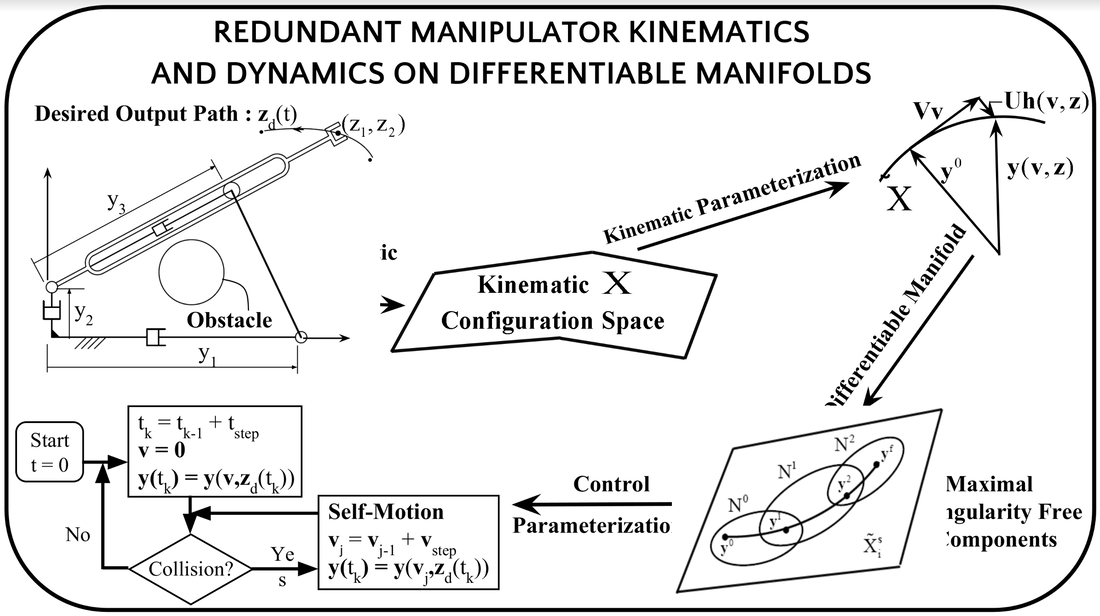
​Redundant manipulators provide versatility and enhance performance potential by using a greater number of inputs than outputs to be controlled. This flexibility enables obstacle avoidance and performance optimization, in addition to achieving specified outputs. However, this requires new analytical and computational tools that enable control strategies that select from an infinite number of admissible inputs that yield the specified output, while realizing enhanced manipulator performance. Topological attributes of Euclidean space, in which manipulators function, are employed to create a differentiable manifold structure that provides explicit parameterization of the infinite number of inputs associated with a desired output. This representation is employed to demonstrate achievement of output specifications, while avoiding obstacles in the manipulator’s workspace by switching between nominal input trajectories far from obstacles to self-motions that prevent collisions otherwise. It is also applied for mapping the self-motion manifold of a seven degree of freedom robot arm that is impossible to analyze using existing methods. A time domain implementation of the parameterization is presented that provides velocity and acceleration information required for control of manipulator dynamics. Computational methods are presented that enable real-time implementation of results derived on modern high-speed microprocessors, for use in computer-based manipulator control systems.

​Edward J. Haug (February 24, 2021). "Multibody Dynamics on Differentiable Manifolds." ASME. J. Comput. Nonlinear Dynam. April 2021; 16(4): 041003. https://doi.org/10.1115/1.4049995
 

​
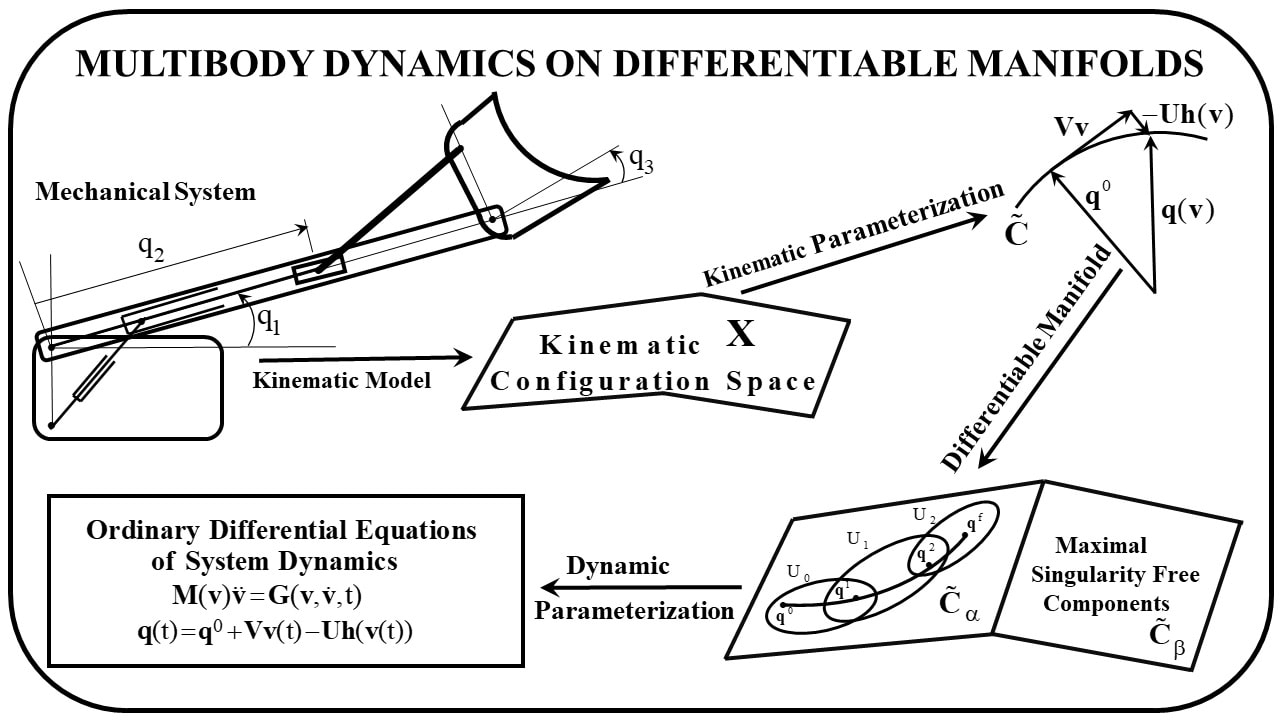
​Topological and vector space attributes of Euclidean space are consolidated from the mathematical literature and employed to create a differentiable manifold structure for multibody kinematics and dynamics. A kinematic configuration space representation of admissible motion of a mechanical system provides the foundation for the development. Using vector space properties of Euclidean space and multivariable calculus, a tangent space kinematic parameterization is presented that establishes the regular configuration space of a multibody system as a differentiable manifold. Topological properties of Euclidean space show that this manifold is naturally partitioned into maximal, singularity free components of kinematic and dynamic functionality. A dynamic parameterization of the d’Alembert variational equation of multibody dynamics yields singularity free ordinary differential equations of system dynamics on these components, without introducing Lagrange multipliers. Solutions of the differential equations satisfy configuration, velocity, and acceleration constraint equations and the variational equations of dynamics; i.e., multibody kinematics and dynamics are embedded in these ordinary differential equations. Two examples, one planar and one spatial, are treated using the formulation presented. Solutions obtained are shown to satisfy all three forms of kinematic constraint to within specified error tolerances, using fourth order Runge-Kutta numerical integration methods.