Archives
February 2024
Categories
All
|
Back to Blog
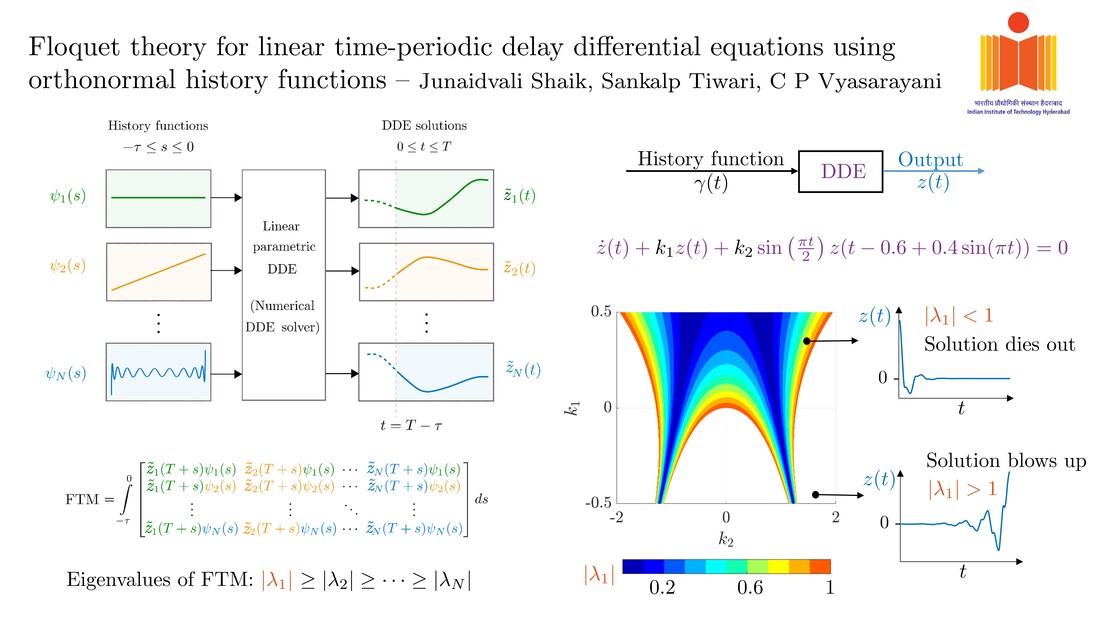
Junaidvali Shaik, Sankalp Tiwari, and C. P. Vyasarayani J. Comput. Nonlinear Dynam. Sep 2023, 18(9): 091005, https://doi.org/10.1115/1.4062633 Delayed systems are those in which the present dynamics is governed by what happened in the past. They are encountered in manufacturing, biology, population dynamics, control systems, etc. Determining linear stability of such systems is an important and difficult problem. In this work, we propose a new method to determine stability of time-periodic delay differential equations (DDEs). In the usual approaches, the DDE is converted into an approximate system of time-periodic ordinary differential equations (ODEs). Later, standard ODE techniques are employed. In this paper, we develop a method that is more direct and general. Our approach is analogous to the well-known Floquet theory for ODEs: we consider one polynomial basis function at a time as the input function and stack the coefficients of the corresponding DDE solutions to construct a matrix whose largest magnitude eigenvalue determines linear stability. We demonstrate the correctness, efficacy and convergence of our method by studying several candidate DDEs with time-periodic parameters and/or delays, and comparing the results with those obtained from other standard methods. Our approach has the following additional advantages: (a) it is parallelizable, (b) it converges quickly, and (c) it requires knowledge of only elementary linear algebra and numerical computation of DDE solutions.
0 Comments
Read More
|
 RSS Feed
RSS Feed