Archives
February 2024
Categories
All
|
Back to Blog
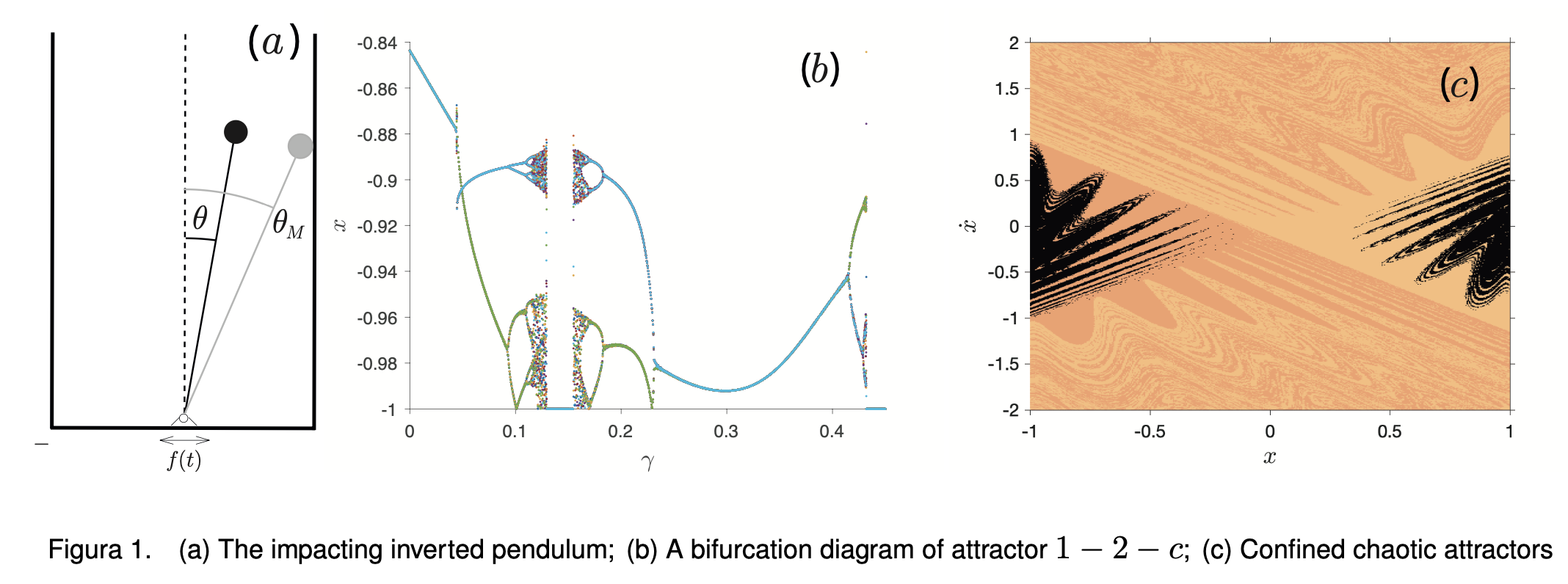
Milena Petrini, Lucio Demeio and Stefano Lenci ASME. J. Comput. Nonlinear Dyn. October 2023, 18(10): 101004 https://doi.org/10.1115/1.4063034 In this work we examine the nonlinear dynamics of an inverted pendulum between lateral rebounding barriers. We continue the numerical investigation started in (Demeio et al., 2006, “Response Scenario and Non-Smooth Features in the Nonlinear Dynamics of an Impacting Inverted Pendulum”, ASME J. Comput. Nonlin. Dyn., 1(1), pp. 56-64) by adding the contribution of the second harmonic in the external forcing term. We investigate the behavior of the periodic attractors by bifurcation diagrams with respect to each amplitude and by behavior charts of single attractors in the amplitude parameters plane for fixed frequency. We study the effects of the second harmonic term on the existence domain of each attractor, on local bifurcations and on the changes in the basins of attraction. The behavior of some robust chaotic attractor is also considered. In the evolution of the periodic attractors we have observed that the addition of the second harmonic generates a rich variety of behaviors, such as loss of stability and formation of isolas of periodic orbits. In the case of chaotic attractors, we have studied one attractor at high frequency, ω = 18, and one at low frequency, ω = 3. In the high frequency case we detect a transition from a scattered to a confined attractor, whereas at the lower frequency the chaotic attractor is present over a wide range of the second harmonic’s amplitude. Finally, we extend the investigation of the chaotic attractors by bifurcation diagrams with respect to the frequency.
0 Comments
Read More
Back to Blog
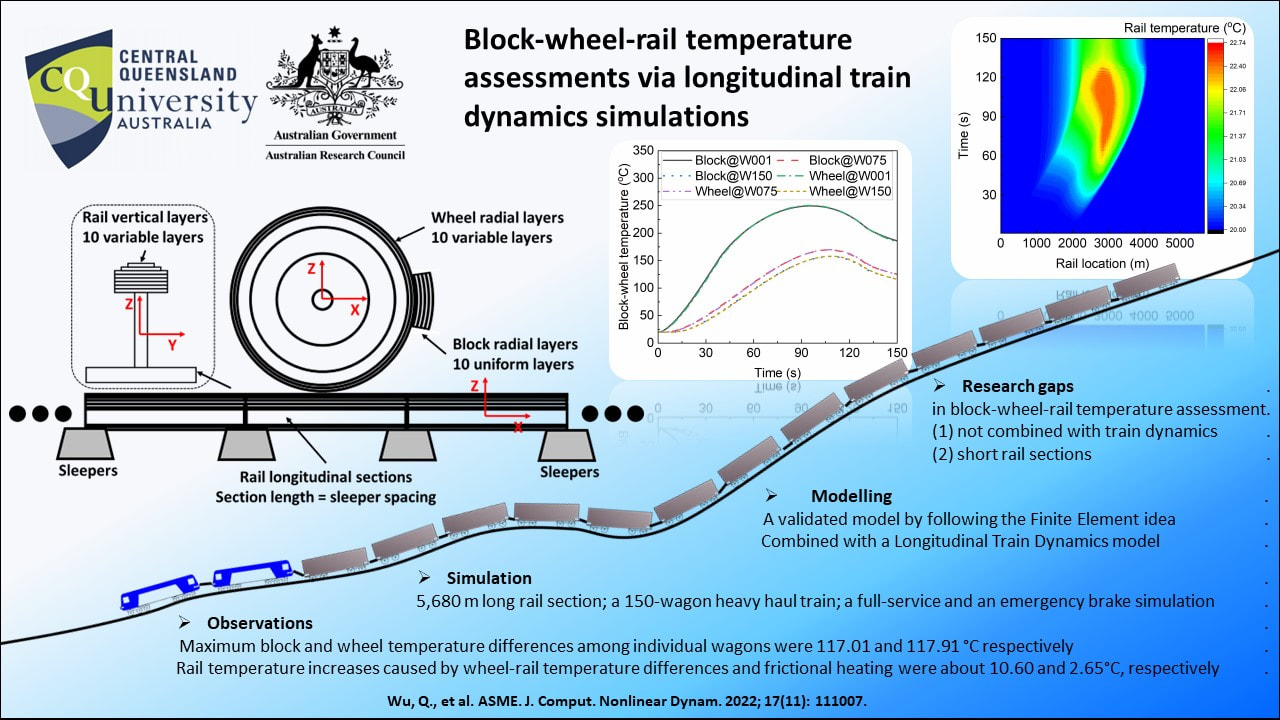
Wu, Q., Spiryagin, M., and Cole, C. (September 16, 2022). "Block–Wheel–Rail Temperature Assessments Via Longitudinal Train Dynamics Simulations." ASME. J. Comput. Nonlinear Dynam. November 2022; 17(11): 111007. https://doi.org/10.1115/1.4055431 Two research gaps were identified in block-wheel-rail temperature assessment. First, current studies are not combined with train dynamics which are better descriptions of the block-wheel-rail working environment. Second, current studies cannot simulate long rail sections. This paper developed a block-wheel-rail temperature assessment model by following the Finite Element idea. Models were validated by comparing with ANSYS Finite Element models and measured data. Case studies were carried out by combining the temperature model with a Longitudinal Train Dynamics model. A full-service and an emergency brake simulation were carried out for a 150-wagon heavy haul train on a 5,680 m long rail section. The results show that, due to brake force differences at different wagon positions, the maximum block and wheel temperature differences among individual wagons in the full-service brake simulation were 117.01 and 117.91 °C respectively. This highlighted the contribution of introducing train dynamics into block-wheel-rail temperature assessment. Rail temperature increases caused by wheel-rail temperature differences and frictional heating were about 10.60 and 2.65°C, respectively.
Back to Blog
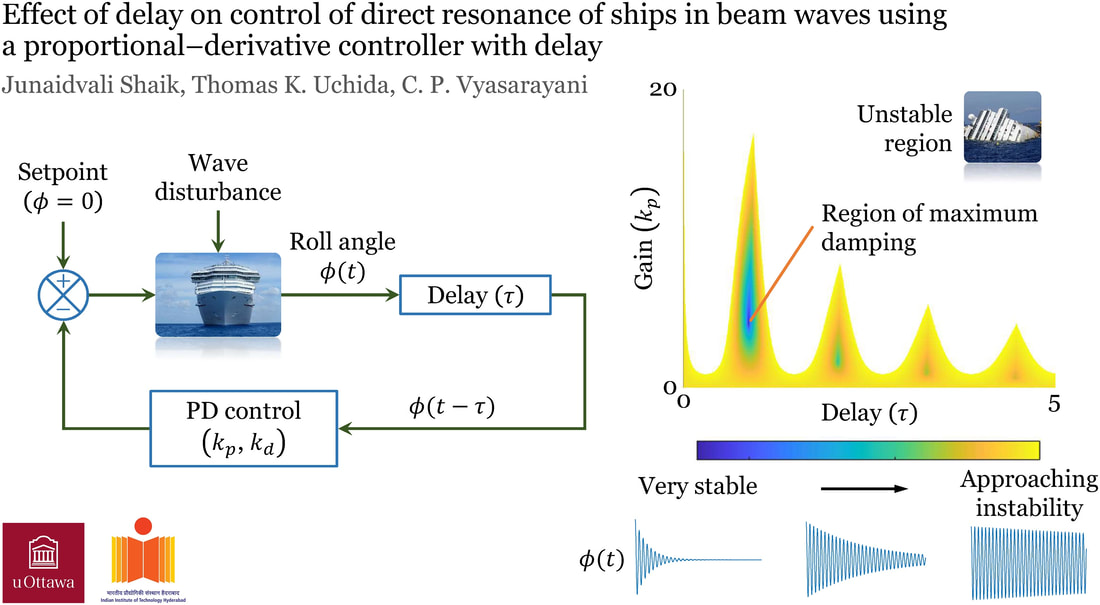
Junaidvali Shaik, Thomas K. Uchida, and C. P. Vyasarayani ASME. J. Comput. Nonlinear Dynam. June 2022; 17(6): 061004. https://doi.org/10.1115/1.4053561 Ships navigating heavy seas are susceptible to various types of wave excitation, which may lead to dynamic instabilities and, in the worst case, capsizing. Compared to the pitch and yaw motions, the roll motion of a ship has the least amount of damping. We study a harmonically excited, single-degree-of-freedom time-delay system with cubic and quintic nonlinearities. This system describes the direct resonance of a ship with an actively controlled anti-roll tank (ART) that is subjected to beam waves, or waves that are approximately perpendicular to the ship’s heading. A proportional–derivative (PD) controller with a constant time delay is assumed to operate the pump in the active ART system. A key result is obtained by deriving the stability boundary of the system, in the parametric space of the control gain and the delay, from the characteristic equation of the linearized system. As shown here, a smaller controller delay is not always better since, in some cases, reducing the delay will reduce the maximum controller gain for which the system is stable. We conduct further analyses using the spectral Tau method, the method of multiple scales, the method of harmonic balance, continuation techniques, and direct numerical simulation.
Back to Blog
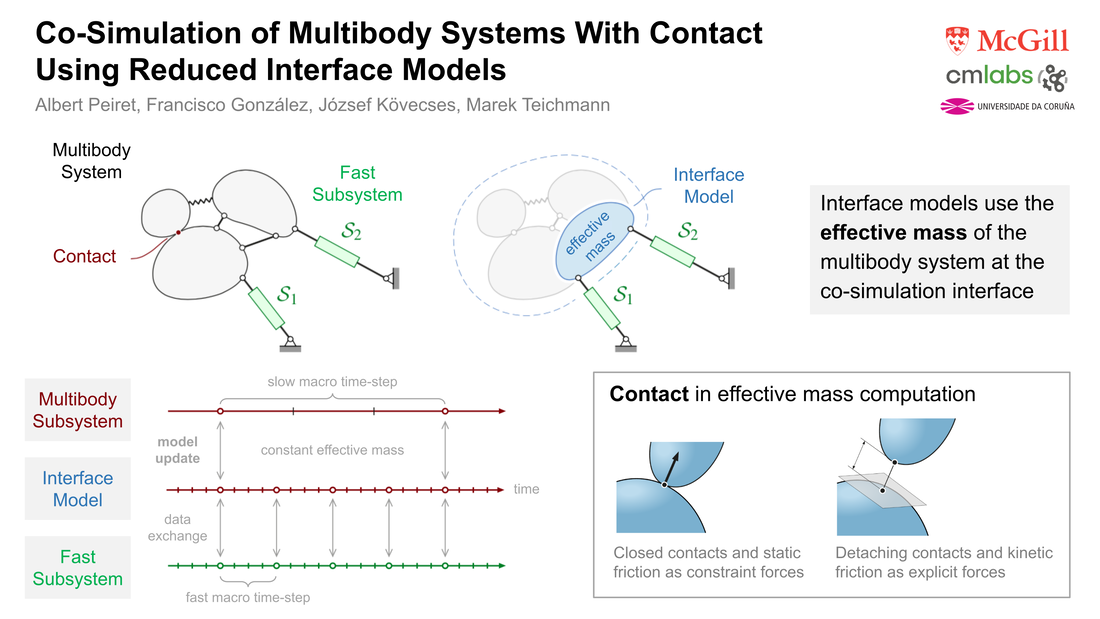
Albert Peiret, Francisco González, József Kövecses, and Marek Teichmann (February 24, 2020). "Co-Simulation of Multibody Systems With Contact Using Reduced Interface Models." ASME. J. Comput. Nonlinear Dynam. April 2020; 15(4): 041001. https://doi.org/10.1115/1.4046052 Co-simulation techniques enable the coupling of models of physically diverse subsystems in an efficient and modular way. Communication between subsystems takes place at discrete time points and is limited to a given set of coupling variables, while the internal details of the subsystems remain undisclosed, and are generally not accessible to the rest of the simulation environment. This can lead to the instability in non-iterative co-simulation that is commonly used in real-time applications. The stability of the simulation in these cases can be enhanced using reduced, effective models of one or more subsystems. These reduced models provide physically meaningful information to the other subsystems between communication points. This work describes such interface models and their application in co-simulation for nonsmooth mechanical systems subjected to unilateral contact and friction. The performance of the proposed approach is shown in some challenging examples of non-iterative, multirate co-simulation interfacing mechanical and hydraulic subsystems. The use of an interface model improves stability and allows for larger integration step-sizes, thus resulting in more efficient simulation.
|
 RSS Feed
RSS Feed