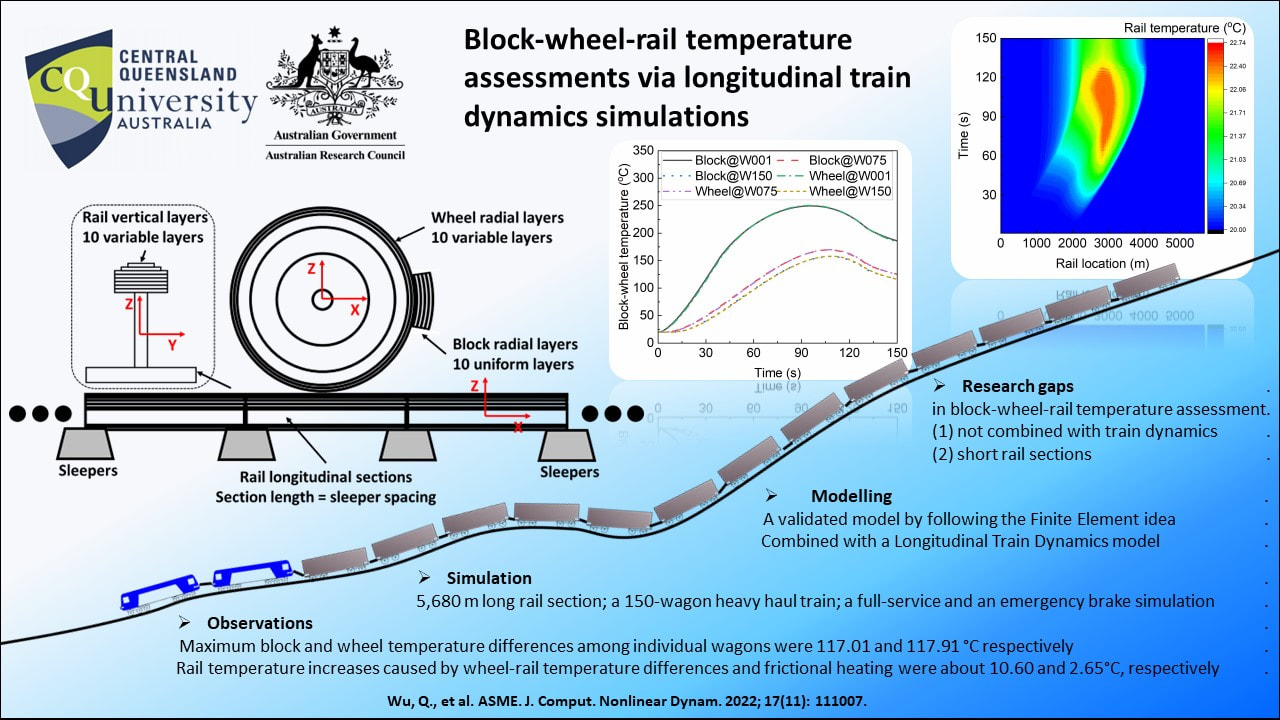
Wu, Q., Spiryagin, M., and Cole, C. (September 16, 2022). "Block–Wheel–Rail Temperature Assessments Via Longitudinal Train Dynamics Simulations." ASME. J. Comput. Nonlinear Dynam. November 2022; 17(11): 111007. https://doi.org/10.1115/1.4055431
​

​Two research gaps were identified in block-wheel-rail temperature assessment. First, current studies are not combined with train dynamics which are better descriptions of the block-wheel-rail working environment. Second, current studies cannot simulate long rail sections. This paper developed a block-wheel-rail temperature assessment model by following the Finite Element idea. Models were validated by comparing with ANSYS Finite Element models and measured data. Case studies were carried out by combining the temperature model with a Longitudinal Train Dynamics model. A full-service and an emergency brake simulation were carried out for a 150-wagon heavy haul train on a 5,680 m long rail section. The results show that, due to brake force differences at different wagon positions, the maximum block and wheel temperature differences among individual wagons in the full-service brake simulation were 117.01 and 117.91 °C respectively. This highlighted the contribution of introducing train dynamics into block-wheel-rail temperature assessment. Rail temperature increases caused by wheel-rail temperature differences and frictional heating were about 10.60 and 2.65°C, respectively.

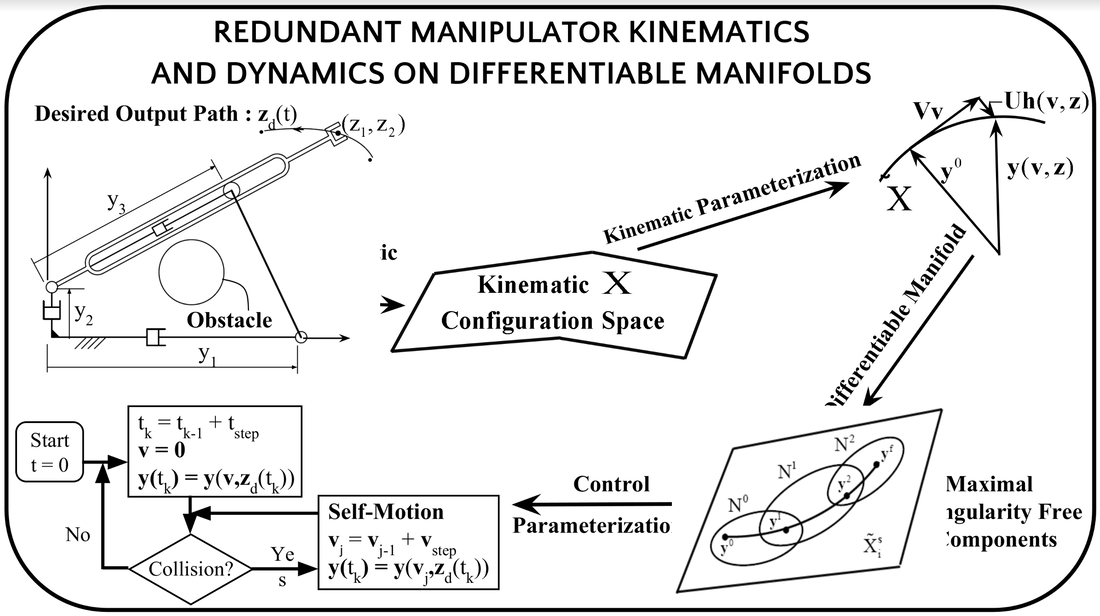
​Redundant manipulators provide versatility and enhance performance potential by using a greater number of inputs than outputs to be controlled. This flexibility enables obstacle avoidance and performance optimization, in addition to achieving specified outputs. However, this requires new analytical and computational tools that enable control strategies that select from an infinite number of admissible inputs that yield the specified output, while realizing enhanced manipulator performance. Topological attributes of Euclidean space, in which manipulators function, are employed to create a differentiable manifold structure that provides explicit parameterization of the infinite number of inputs associated with a desired output. This representation is employed to demonstrate achievement of output specifications, while avoiding obstacles in the manipulator’s workspace by switching between nominal input trajectories far from obstacles to self-motions that prevent collisions otherwise. It is also applied for mapping the self-motion manifold of a seven degree of freedom robot arm that is impossible to analyze using existing methods. A time domain implementation of the parameterization is presented that provides velocity and acceleration information required for control of manipulator dynamics. Computational methods are presented that enable real-time implementation of results derived on modern high-speed microprocessors, for use in computer-based manipulator control systems.