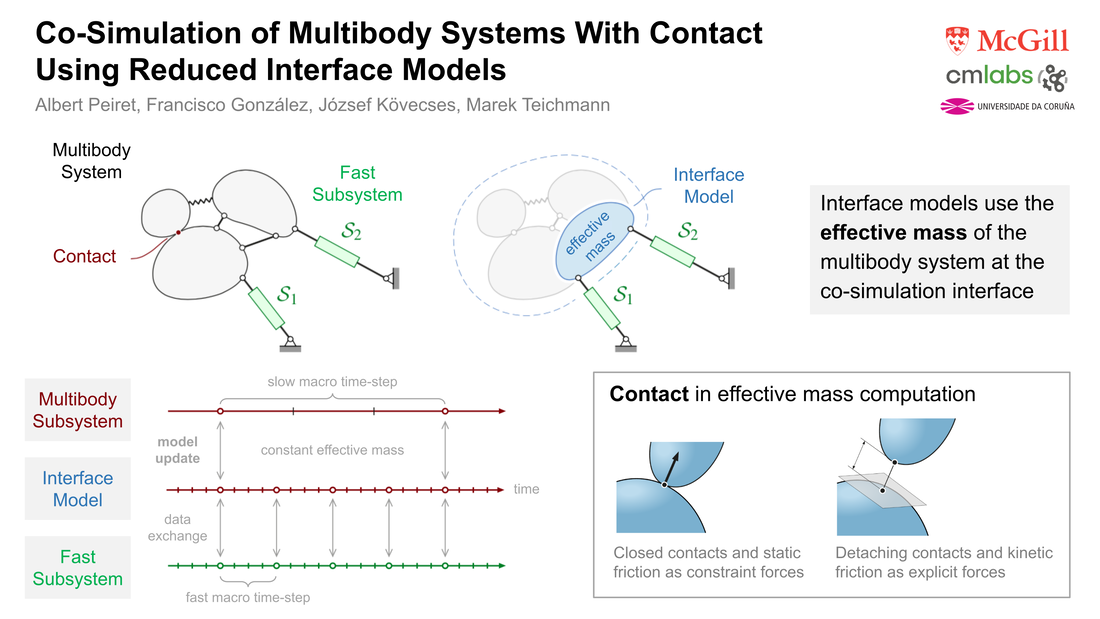
Albert Peiret, Francisco González, József Kövecses​, and Marek Teichmann (February 24, 2020). "Co-Simulation of Multibody Systems With Contact Using Reduced Interface Models." ASME. J. Comput. Nonlinear Dynam. April 2020; 15(4): 041001. https://doi.org/10.1115/1.4046052

Co-simulation techniques enable the coupling of models of physically diverse subsystems in an efficient and modular way. Communication between subsystems takes place at discrete time points and is limited to a given set of coupling variables, while the internal details of the subsystems remain undisclosed, and are generally not accessible to the rest of the simulation environment. This can lead to the instability in non-iterative co-simulation that is commonly used  in real-time applications. The stability of the simulation in these cases can be enhanced using reduced, effective models of one or more subsystems. These reduced models provide physically  meaningful information to the other subsystems between communication points.  This work describes such interface models and their application in co-simulation for nonsmooth mechanical systems subjected to unilateral contact and friction. The performance of the proposed approach is shown in some challenging examples of non-iterative, multirate co-simulation interfacing mechanical and hydraulic subsystems. The use of an interface model improves stability and allows for larger integration step-sizes, thus resulting in more efficient simulation. 

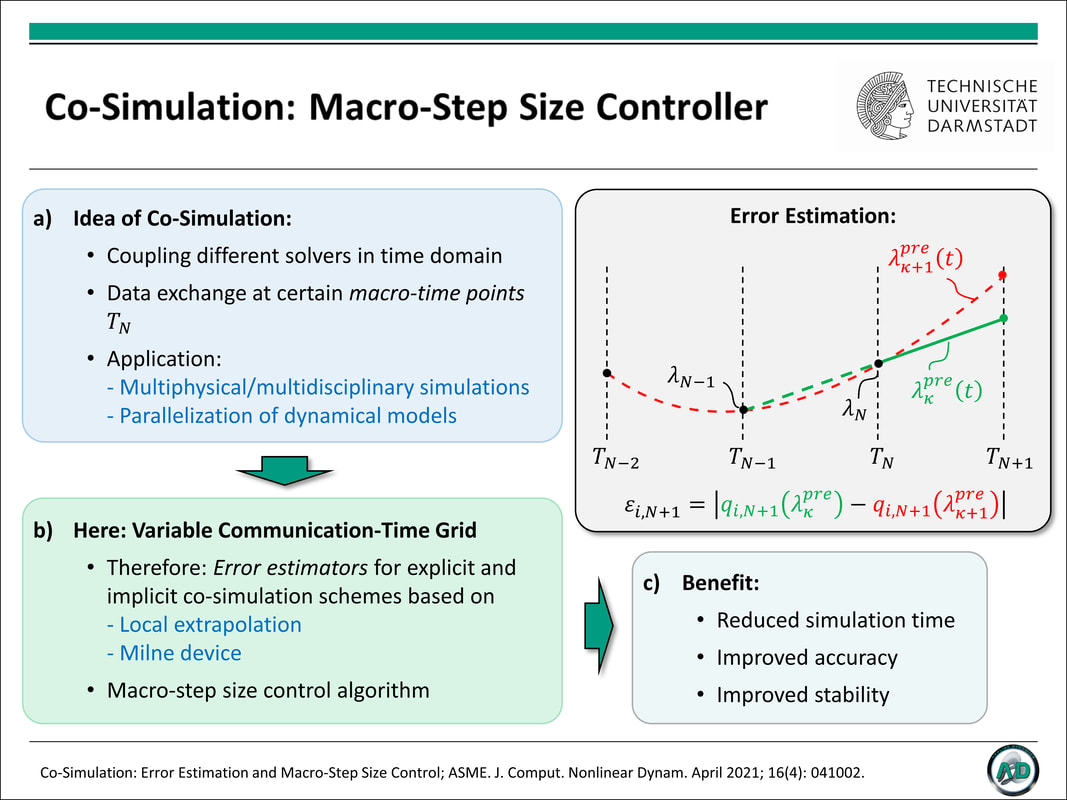
T. Meyer, J. Kraft,  and B. Schweizer (February 24, 2021). "Co-Simulation: Error Estimation and Macro-Step Size Control." ASME. J. Comput. Nonlinear Dynam. April 2021; 16(4): 041002. https://doi.org/10.1115/1.4048944

Co-simulation techniques are commonly used to analyze multidisciplinary and multiphysical systems as well as to parallelize dynamical simulation models. Therefore, the overall system is decomposed into a certain number of subsystems. To define the coupling between the subsystems, coupling equations and appropriate coupling variables have to be specified. Moreover, a communication-time grid has to be introduced by defining macro-time points . The subsystems are integrated independently between the communication-time points; coupling variables are only exchanged at the macro-time points. The crucial point in connection with equidistant communication-time grids, which are frequently used in practical applications, is the appropriate choice of the macro-step size. Efficiency and accuracy of a co-simulation may, however, considerably be increased by using a variable communication-time grid. Therefore, an error estimator for controlling the macro-step size is required. Here, different error estimators for explicit and implicit co-simulation schemes are derived and incorporated into the macro-step size control algorithm. Numerical studies clearly demonstrate that the main problems associated with equidistant macro-grids – namely a trade-off between stability/accuracy and efficiency – disappear, if variable communication-time grids are used. The manuscript focuses on mechanical co-simulation models. The basic results may, however, also be applied to arbitrary, non-mechanical co-simulation models.