Period-1 Motions to Twin Spiral Homoclinic Orbits in the Rössler System

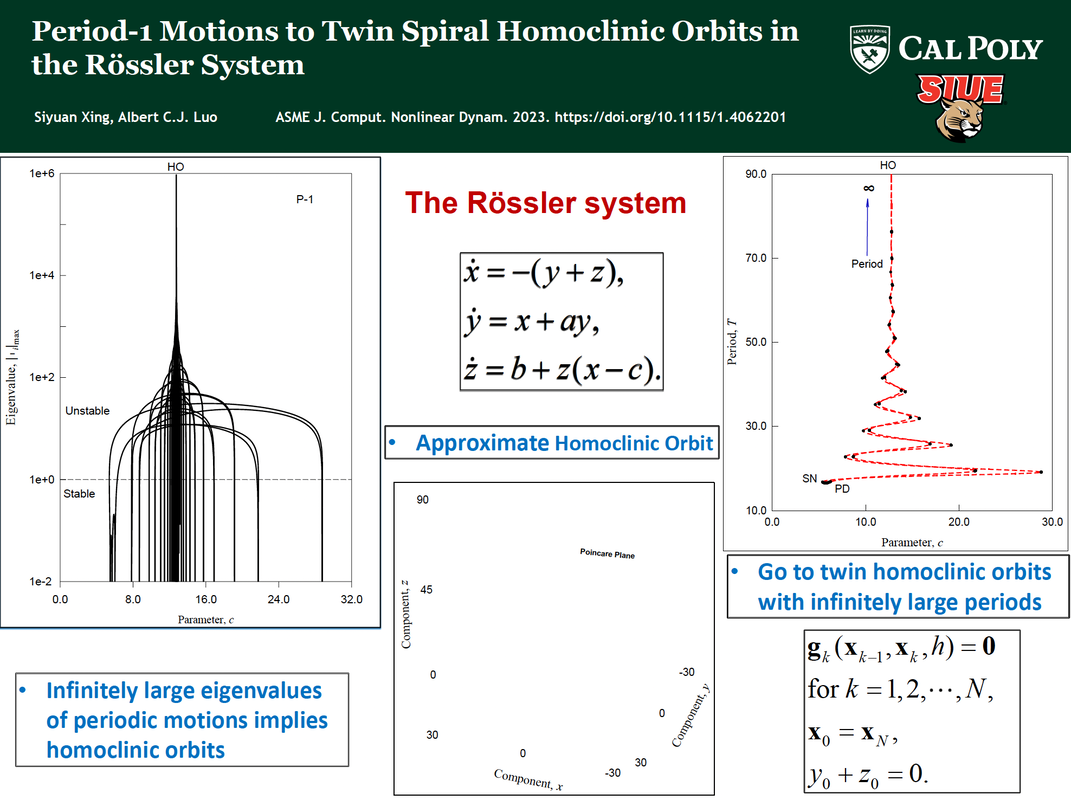
Siyuan Xing and Albert C. J. Luo, Period-1 Motions to Twin Spiral Homoclinic Orbits in the Rössler System, J. Comput. Nonlinear Dynam. Aug 2023, 18(8): 081008. https://doi.org/10.1115/1.4062201

​The Rössler system was proposed as one of the simplest three-dimensional nonlinear systems in order to exhibit chaotic behaviors in 1976. Since then, extensive qualitative and quantitative research on such a system has been conducted to study the mathematical structures of periodic orbits in the vicinity of homoclinic orbits. Many advances in this field have been achieved through the linearized, approximate theory and numerical studies, but it is still far away to completely solve the problem. In this paper, the periodic motions of the Rössler system are predicted through an implicit mapping method, and the corresponding stability of periodic motions is determined by eigenvalue analysis. The semi-analytical bifurcation tree from periodic motions to two spiral homoclinic orbits is obtained. The unstable periodic motions with fast-slow movements are accurately predicted. Homoclinic orbits are identified through infinitely large eigenvalues. The approximate homoclinic orbits with different periods are presented for a better understanding of the spiral homoclinic orbits spiraling out from the saddle-focus equilibriums.  

Full Paper