Archives
February 2024
Categories
All
|
Back to Blog
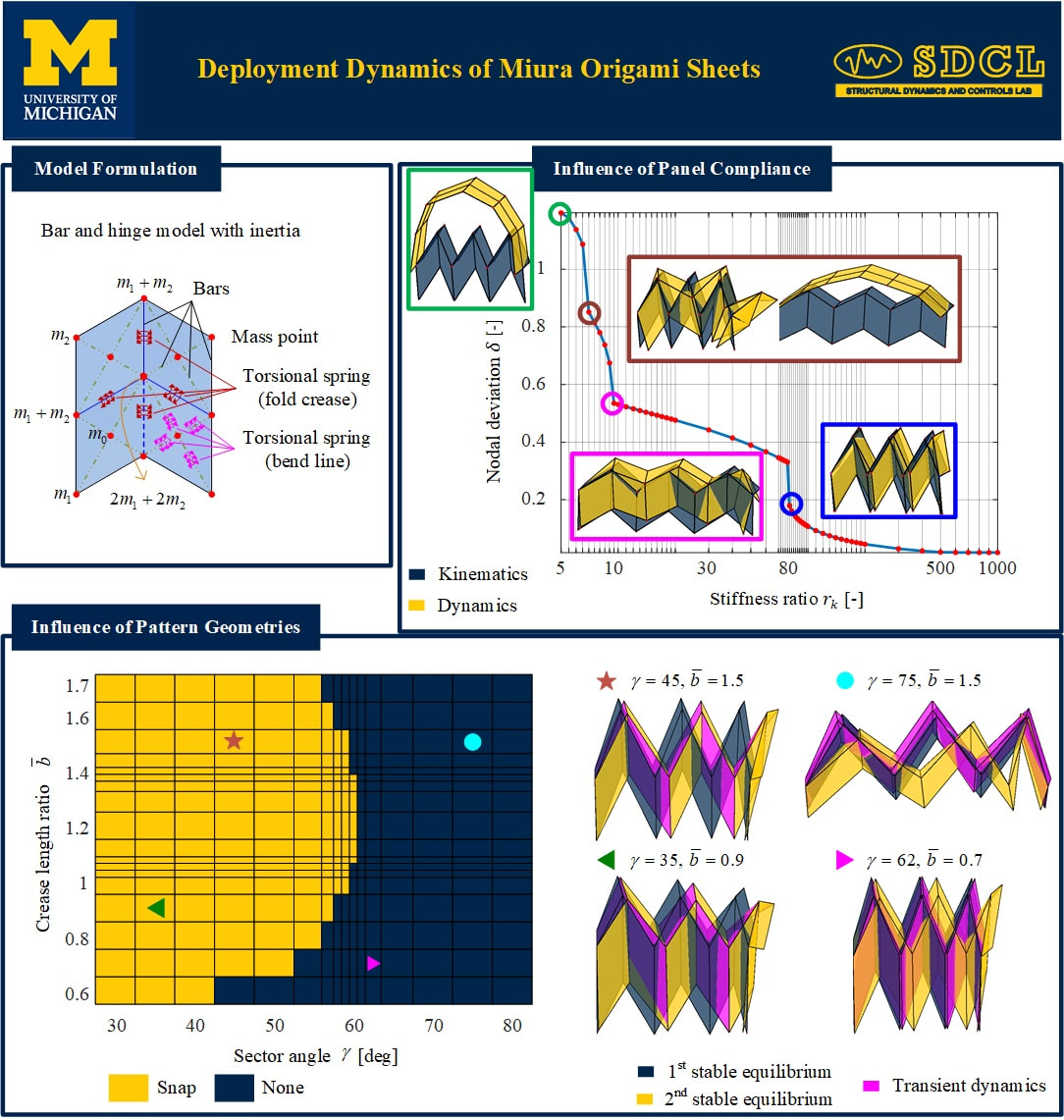
Yutong Xia, Narayanan Kidambi, Evgueni Filipov, K. W. Wang, "Deployment Dynamics of Miura Origami Sheets" ASME. J. Comput. Nonlinear Dynam. Jul 2022, 17(7): 071005. https://doi.org/10.1115/1.4054109 Origami is an ancient paper-folding art that can transform a two-dimensional (2-D) sheet into a complex 3-D structure. It has emerged as a promising tool for the design of mechanical structures with various functionalities. Because origami principles are scale independent, they can be adopted for the designs from large-scale space structures such as origami-based inflatable boom and antenna, to mesoscale origami robots, and to micro-scale medical devices. The foldability property allows for easy fabrication, compact storage, and easy transportation because origami can be compactly folded into small volumes and then unfolded to become large systems. Most studies have focused on static or kinematic deployment process of origami structures, while it is important to understand the deployment dynamics to achieve desired performances and mitigate safety concerns. In this research, we construct a dynamic model of a Miura origami sheet that captures the combined panel inertial and flexibility effects, which are otherwise ignored in rigid folding kinematic models but are critical in describing the dynamics of origami deployment. Results show that by considering these effects, the dynamic deployment behavior would substantially deviate from a nominal kinematic unfolding path. Additionally, the pattern geometries influence the effective structural stiffness, and it is shown that subtle changes can result in qualitatively different dynamic deployment behaviors. These differences are due to the multistability of the Miura origami sheet, where the structure may snap between its stable equilibria during the transient deployment process. Lastly, we show that varying the deployment rate can affect the dynamic deployment configuration. These observations are original and these phenomena have not and cannot be derived using traditional approaches. The tools and outcomes developed from this research enable a deeper understanding of the physics behind origami deployment that will pave the way for better designs of origami-based deployable structures, as well as extend our fundamental knowledge and expand our comfort zone beyond current practice.
0 Comments
Read More
|
 RSS Feed
RSS Feed