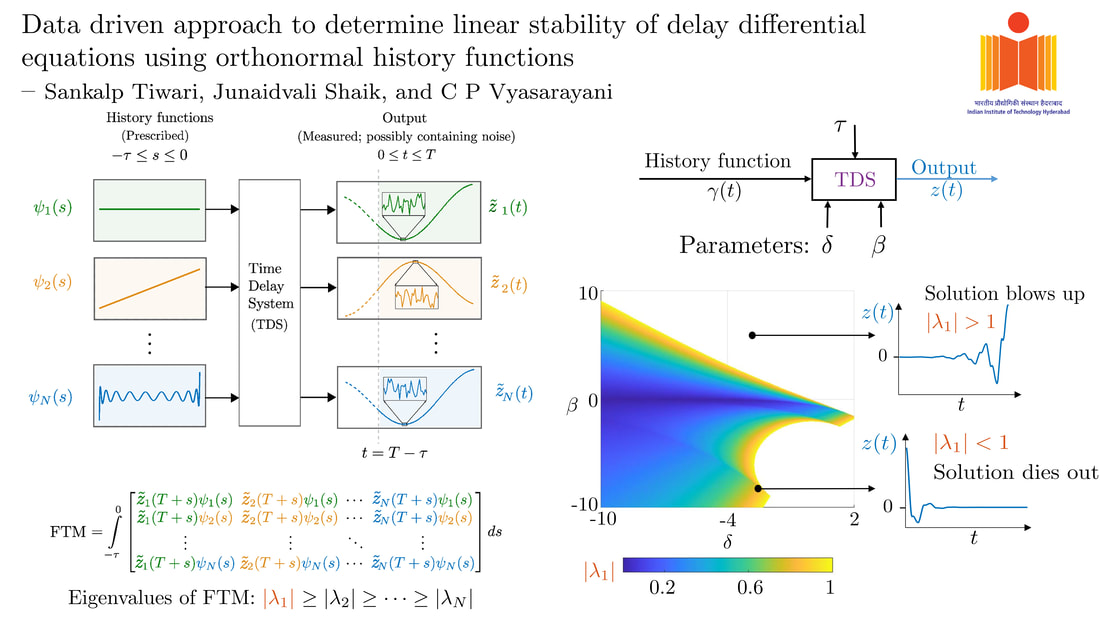
Sankalp Tiwari, Junaidvali Shaik, and C. P. Vyasarayani
J. Comput. Nonlinear Dynam. Feb 2024, 19(2): 021002 
​https://doi.org/10.1115/1.4064251

​Delayed systems are those in which the present dynamics is governed by what happened in the past. They are encountered in manufacturing, biology, population dynamics, control systems, etc. Determining stability of such systems is an important and difficult problem. In the existing works, stability is determined by assuming the governing differential equation. However, the equation may not be known or difficult to obtain. Unlike existing works, our method determines the linear stability of a delayed system using its response to a few known inputs. In particular, our method does not require or assume the differential equation governing that system. The only system information we use is its largest delay time, and the only assumption we make about the underlying equation is that its coefficients are either constant or time-periodic. Our approach involves giving the first few functions of an orthonormal polynomial basis as input and measuring/computing the corresponding responses to generate a state transition matrix, whose largest eigenvalue determines the stability. We demonstrate our method's correctness, efficacy, and convergence by studying four candidate DDEs with differing features. Importantly, we show that our approach is robust to noise in measurement, thereby establishing its suitability for practical applications.

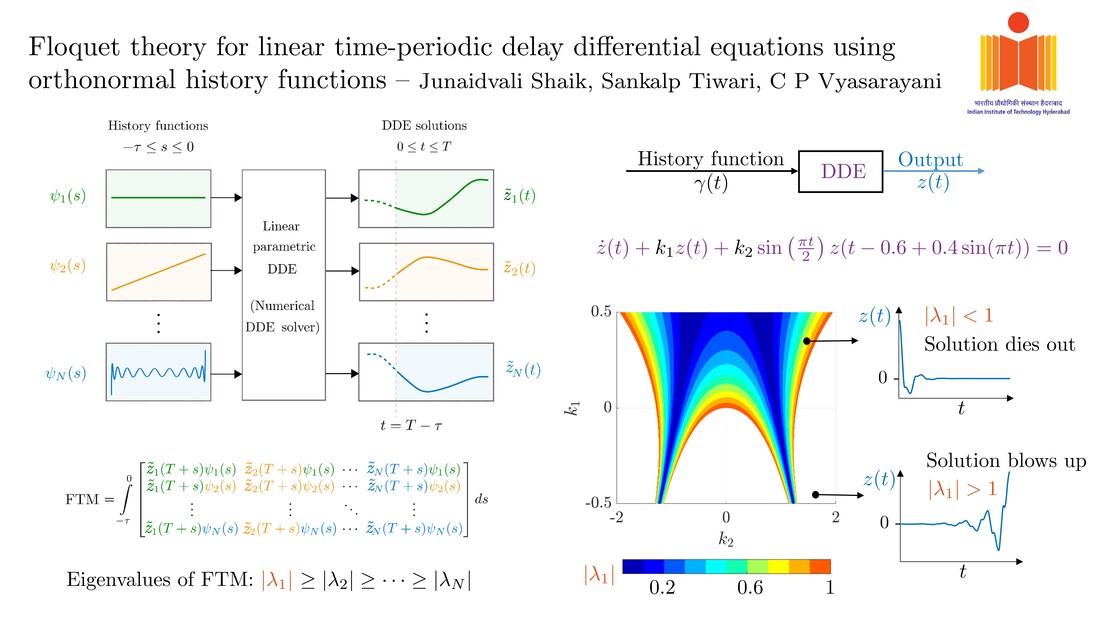
Junaidvali Shaik, Sankalp Tiwari, and C. P. Vyasarayani
J. Comput. Nonlinear Dynam. Sep 2023, 18(9): 091005, https://doi.org/10.1115/1.4062633​

Delayed systems are those in which the present dynamics is governed by what happened in the past. They are encountered in manufacturing, biology, population dynamics, control systems, etc. Determining linear stability of such systems is an important and difficult problem. In this work, we propose a new method to determine stability of time-periodic delay differential equations (DDEs). In the usual approaches, the DDE is converted into an approximate system of time-periodic ordinary differential equations (ODEs). Later, standard ODE techniques are employed. In this paper, we develop a method that is more direct and general. Our approach is analogous to the well-known Floquet theory for ODEs: we consider one polynomial basis function at a time as the input function and stack the coefficients of the corresponding DDE solutions to construct a matrix whose largest magnitude eigenvalue determines linear stability. We demonstrate the correctness, efficacy and convergence of our method by studying several candidate DDEs with time-periodic parameters and/or delays, and comparing the results with those obtained from other standard methods. Our approach has the following additional advantages: (a) it is parallelizable, (b) it converges quickly, and (c) it requires knowledge of only elementary linear algebra and numerical computation of DDE solutions. ​

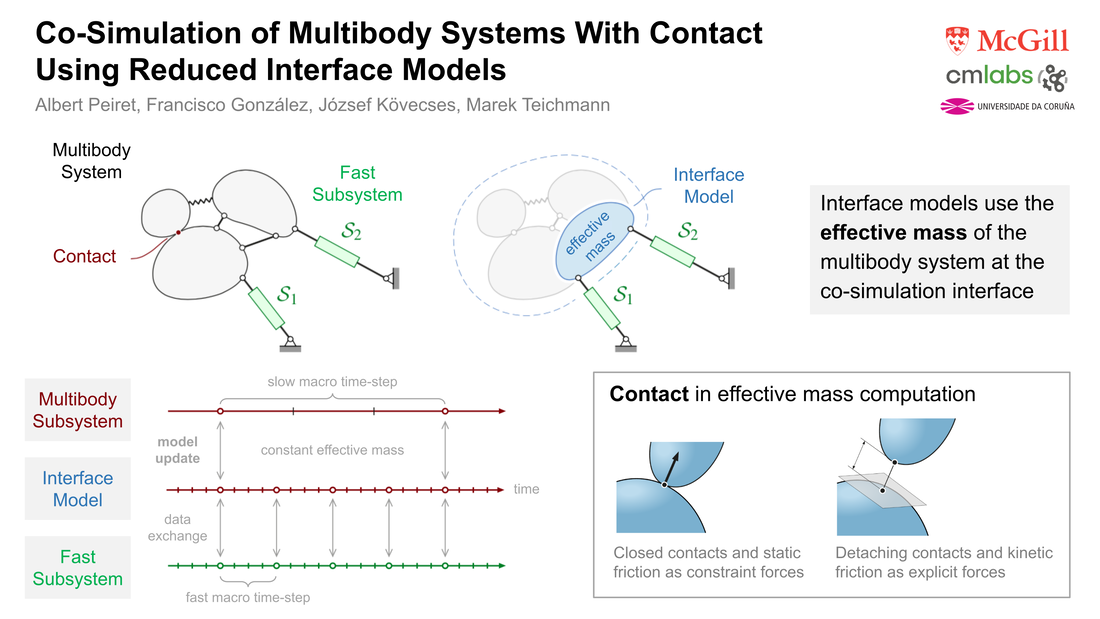
Albert Peiret, Francisco González, József Kövecses​, and Marek Teichmann (February 24, 2020). "Co-Simulation of Multibody Systems With Contact Using Reduced Interface Models." ASME. J. Comput. Nonlinear Dynam. April 2020; 15(4): 041001. https://doi.org/10.1115/1.4046052

Co-simulation techniques enable the coupling of models of physically diverse subsystems in an efficient and modular way. Communication between subsystems takes place at discrete time points and is limited to a given set of coupling variables, while the internal details of the subsystems remain undisclosed, and are generally not accessible to the rest of the simulation environment. This can lead to the instability in non-iterative co-simulation that is commonly used  in real-time applications. The stability of the simulation in these cases can be enhanced using reduced, effective models of one or more subsystems. These reduced models provide physically  meaningful information to the other subsystems between communication points.  This work describes such interface models and their application in co-simulation for nonsmooth mechanical systems subjected to unilateral contact and friction. The performance of the proposed approach is shown in some challenging examples of non-iterative, multirate co-simulation interfacing mechanical and hydraulic subsystems. The use of an interface model improves stability and allows for larger integration step-sizes, thus resulting in more efficient simulation. 

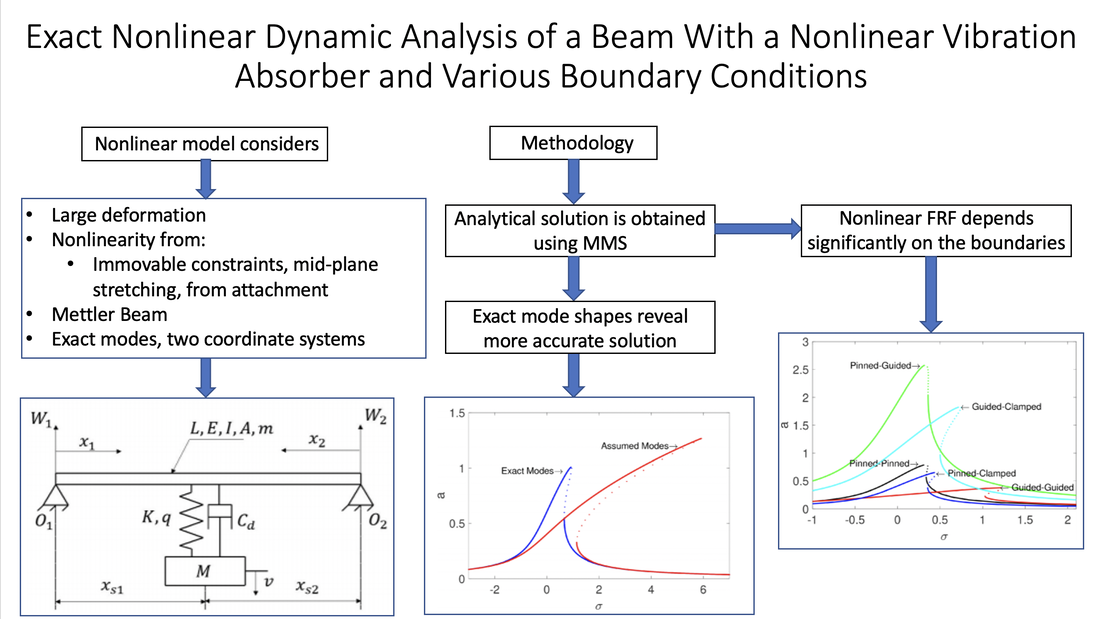
Mohammad Bukhari and Oumar Barry (November 11, 2019). "Exact Nonlinear Dynamic Analysis of a Beam With a Nonlinear Vibration Absorber and With Various Boundary Conditions." ASME. J. Comput. Nonlinear Dynam. January 2020; 15(1): 011003. https://doi.org/10.1115/1.4045287

Beams are the basic component of many engineering applications. They are used in bridges, overhead transmission lines, pipelines, sensors, aircraft structures, and many others. To ensure safety and proper function, vibrations of beams need to be investigated for better prediction of the system dynamical response. When the vibration amplitude is small, linear theory can predict the response accurately. However, when the vibration amplitude becomes larger, nonlinearity must be considered to avoid erroneous results. This work investigates the nonlinear vibration of a beam with attached Nonlinear Vibration Absorber (NVA) consisting of a spring-mass system). The considered nonlinearity stems from mid-plane stretching due to immovable boundary conditions and from the nonlinear stiffness in the NVA. In addition, different types of immovable boundary are investigated. For weak nonlinearity, an approximate analytical solution is derived using the method of multiple scales. These analytical results are validated using direct numerical integration. Parametric studies demonstrate that the performance of the NVA does not only depend on its key design variables and location, but also on the beam boundary conditions, midplane stretching of the beam, and NVA configuration (i.e., grounded versus ungrounded). Our analysis also indicates that the common approach of employing approximate modes in estimating the nonlinear response of a loaded beam produces significant error, up to 1200% in some cases. These findings could contribute to the design improvement of NVAs, microelectromechanical systems (MEMS), energy harvesters, and metastructures. 

​

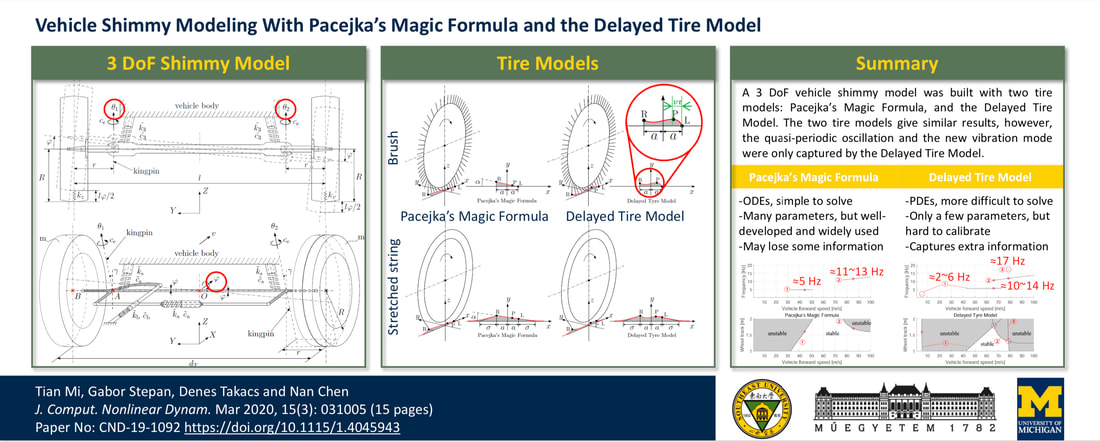
Shimmy is a self-excited vibration which can appear in various wheeled mechanisms such as trailers, motorcycles, bicycles, cars, landing gears of aircrafts, and even baby strollers or supermarket trolleys. Shimmy of cars is also known as vehicle shimmy or death wobble. The cause of shimmy is related to the dynamic characteristics of the tire-road contact and the overall system structure. It increases tire wear, deteriorates vehicle handling, and causes further instability problems of the whole vehicle.

In this paper, a 3 degree-of-freedom model of vehicle front wheels with dependent suspension is studied from the viewpoint of possible appearance of shimmy, and two tire models are compared. The two tire models have essentially different assumptions: Pacejka’s magic formula uses linearization in space along the tire-ground contact line where the tire points stick to the ground, while the delayed tire model uses linearization in time by considering small (but spatially nonlinear) lateral deformations of the tire in the contact region. The theoretical results show that the delayed tire model presents additional instabilities (i.e., shimmy) at low speeds, and especially at low damping values.

The investigation of this model is motivated by the occurrence of shimmy on some heavy vehicles and jeeps with worn front wheel suspension system, and the conclusions might be useful in the future study of shimmy in systems with independent suspensions of some electric vehicles.