Archives
February 2024
Categories
All
|
Back to Blog
Harry Dankowicz, Yuqing Wang, Frank Schilder, and Michael E. Henderson (March 18, 2020). "Multidimensional Manifold Continuation for Adaptive Boundary-Value Problems." ASME. J. Comput. Nonlinear Dynam. May 2020; 15(5): 051002. https://doi.org/10.1115/1.4046498 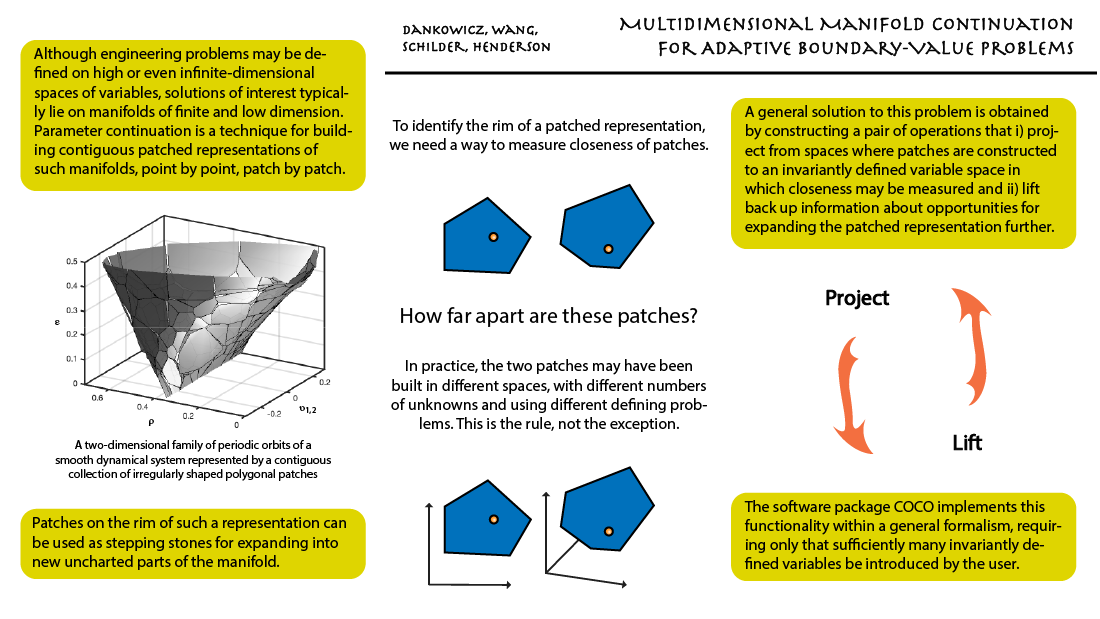 Problems of engineering analysis are often formulated as systems of nonlinear equations that impose dependencies among the unknown variables. Even as the numbers of unknowns and equations may be very large, or even infinite, the number of degrees of freedom is typically finite and small. This is true of boundary-value problems corresponding to periodic orbits of smooth dynamical systems. Here, the number of degrees of freedom equals the number of system parameters, even though the space of unknown variables is infinite-dimensional. It is rarely possible to describe all solutions of a system of nonlinear equations in terms of a single set of independent variables, equal in number to the number of degrees of freedom. It is, however, typically possible to construct a marginally larger set of dependent variables that accomplishes this goal. Such a single set of variables may also be used to describe and compare approximate solutions to an infinite-dimensional problem obtained using different discretizations or different parameterizations of the governing equations. This idea is implemented in the most recent release of the software package COCO, a parameter continuation tool for approximating finite-dimensional manifolds of solutions to nonlinear equations by successively expanding piecewise-flat covers of such manifolds. Uniquely to this tool, analysis can proceed even when the problem discretization and parameterization vary during continuation, for example, when adapting a mesh to accommodate constraints on estimated discretization errors. As demonstrated in this paper, orders of magnitude reductions in computational costs result from judicious variable choices and degeneracies associated with phase invariances, as occur for periodic response of autonomous systems, can be eliminated with or without additional phase conditions.
0 Comments
Read More
|
 RSS Feed
RSS Feed

